Link Copied!

Normalizing Flow 부터 Continuous Normalizing Flow 와 Conditional Flow Matching, 그리고 Rectitifed Flow 가 왜 Linear Path 를 채택하는지 수학적, 물리적으로 상세하게 이해해보자.
Flow Matching 은 그 이론적 깊이 때문에 쉽게 접근할 수 있는 설명 자료가 아직 부족합니다. 많은 연구자, 개발자들이 '왜 하필 직선 경로가 효과적인가?' 라는 근본적인 질문에 대한 깊이 있는 직관을 갖기는 어렵습니다. 이 글은 그런 실정에서 수학, 물리학, 그리고 최신 논문에 흩어져 있는 Flow Matching 의 핵심 아이디어들을 하나의 유기적인 이야기로 엮어내어, Flow Matching 의 'Why' 에 대한 직관을 얻어 가는 것을 목표로 삼고 씌여졌습니다.

Introduction

최근 생성 모델의 흐름은 크게 두 가지 접근법으로 나눌 수 있다.

하나는 노이즈에서부터 점차 이미지를 생성해나가는 Diffusion Model 이고, 다른 하나는 노이즈와 이미지를 직접적으로 잇는 Flow 기반 모델이다.

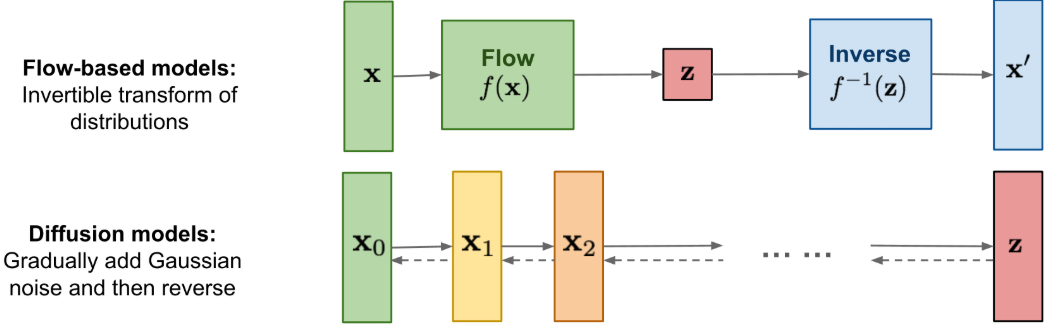
특히 Diffusion Model 은 복잡한 Stochastic Differential Equation (SDE) 을 기반으로 한다. 이는 마치 입자가 무작위적인 힘에 의해 이리저리 흔들리며 움직이는 'Brownina Motion' 처럼, 구불구불하고 예측 불가능한 경로를 통해 샘플을 생성하는 방식이다. 이는 뛰어난 성능을 보였지만, 본질적으로 수많은 단계를 거쳐야 하기 때문에 느린 생성 속도라는 단점을 안고 있었다.

이러한 배경 속에서, "더 빠르고, 더 효율적인 생성 방법은 없을까?"라는 질문에 대한 대답으로 Ordinary Differential Equation (ODE) 기반의 framework 가 주목받기 시작했다. ODE 는 SDE 와 달리 무작위성 (stochastic) 이 배제된 deterministic path 를 따른다. 즉, 출발점과 도착점이 정해지면 그 사이의 경로는 단 하나로 명확하게 결정된다.

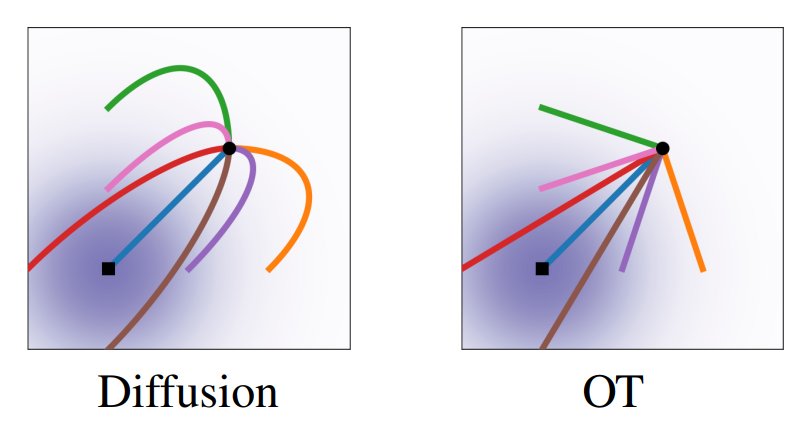
Top: Diffusion <-> Middle & Bottom: Flow-Matching. Stochastic 과 deterministic 의 차이를 잘 볼 수 있다.

이 단순하고 강력한 아이디어를 기반으로 한 Rectified Flow 는 등장과 함께 가장 주목받는 state-of-the-art 생성 프레임워크 중 하나로 자리 잡았다. Rectified Flow 는 노이즈 $z_0$ 와 target $z_1$ 사이의 무수히 많은 가능한 ODE 경로 중, 가장 단순한 직선 경로를 가정한다. 이 덕분에 학습은 안정화되고 샘플링 속도는 비약적으로 빨라졌다.

이번 글에서는 이 ODE 기반 생성 모델의 한 축을 담당하는 Flow Matching 에 대해 먼저 알아보며, 그 중 한 형태인 Rectified Flow 가 왜 그토록 단순하고 강력한 '직선 경로' 를 채택했는지 파헤치기 위해 Optimal Transport 이론까지 깊이 살펴보도록 하겠다.

Part A. Flow Matching

1. Normalizing Flow

1.1. What is Flow

Flow 기반 모델의 아이디어는 단순하고 우아하다.

"쉽게 다룰 수 있는 단순한 확률 분포 (e.g., gaussian distribution) 를, 어떤 복잡하지만 근사하고 싶은 실제 데이터 분포로 '변환'하는 함수를 학습할 수 있을까?"

이 '변환 함수' $\phi$ 를 학습하는 과정 자체를 Normalizing Flow 라고 부른다.

Input: noise distribution $p_0$ 에서 뽑은 샘플 $x_0$
Output: 변환 함수를 통과한 결과 $x_1 = \phi(x_0)$
Goal: 이 결과물 $x_1$의 분포가 real data distribution $p_1$ 과 같아지도록, 즉 그럴듯한 이미지가 생성되도록 $\phi$ 를 학습시킨다.

따라서, 학습 목표는 $$ \phi(x_0) = x_1 \sim p_1 $$ 관계를 만족하는 continuous, differentiable, invertible 한 mapping function $\phi$ 를 찾는 것이다.

이 목표를 달성하려면, 변환된 샘플 $x_1$이 데이터 분포 $p_1$에 속할 확률, 즉 likelihood $p_1(x_1)$ 을 계산하고 이를 최대화해야 한다.

1.2. Likelihood of Normalizing Flow

이제 Change of Variables Theorem 를 이용하여 $x_1$ 과 $x_0$ 의 관계를 정리하면, 변환 $\phi$ 전후의 infinitesimal probability 이 동일해야한다는 관계를 얻는다 (probability mass).

$$ p_1(x_1)|dx_1| = p_0(x_0)|dx_0| $$

이를 $p_1(x_1)$ 에 대해 정리하고, $x_0 = \phi^{-1}(x_1)$ 관계를 이용해 정리하면 다음과 같다.

$$ p_1(x_1) = p_0(\phi^{-1}(x_1)) \left| \det\left( \frac{\partial \phi^{-1}(x_1)}{\partial x_1} \right) \right| $$

non-linear function $\phi^{-1}$ 는 $x_1$ 근방에서 국소적으로 linear transformation 으로 근사할 수 있을 것이다. 이 국소적 선형 변환을 나타내는 행렬이 바로 Jacobian
$$ J_{\phi^{-1}}(x_1) = \frac{\partial \phi^{-1}(x_1)}{\partial x_1} $$ 이다.
여기서 $\det(\cdot)$ 는 변환에 따른 space 의 부피 변화를 보정해주는 값인데, 선형 대수학에서 한 선형 변환이 공간의 부피를 얼마나 변화시키는지는, 그 변환을 나타내는 행렬의 determinant 값으로 측정되기 때문이다 (cf: Geometric Meaning of the Determinant).

이 식의 양변에 로그를 취하면, 우리가 loss function 으로 사용하여 최대화해야 할 log-likelihood 를 얻게 된다.

$$ \log p_1(x_1) = \log p_0(\phi^{-1}(x_1)) + \log \left| \det\left( \frac{\partial \phi^{-1}(x_1)}{\partial x_1} \right) \right| $$

하지만 이 접근법에는 두 가지 큰 난관이 존재한다.

Invertibility: 변환 함수 $\phi$ 의 역함수 $\phi^{-1}$ 를 계산할 수 있어야 한다.
계산 비용: Jacobian determinant 의 계산 비용$\mathcal{O}(D^3)$ 이 너무 커서 고차원 데이터에는 적용하기 어렵다.

2. Continuous Normalizing Flow

2.1. Continuous Flow

이 문제를 해결하기 위해,

"하나의 거대한 변환 함수 $\phi$ 대신, 아주 작은 변화들을 무한히 연결한 'Flow' 로 생각하면 어떨까?"

라는 아이디어가 등장했다.

이는 변환 과정을 시간의 흐름에 따른 continuous trajectory 으로 모델링하는 것을 의미한다.

이 trajectory 위에서 샘플 $x_0$ 은 시간 $t=0$ 에서의 위치이고, 우리가 원하는 데이터 $x_1$ 는 시간 $t=1$ 에서의 최종 위치가 된다.

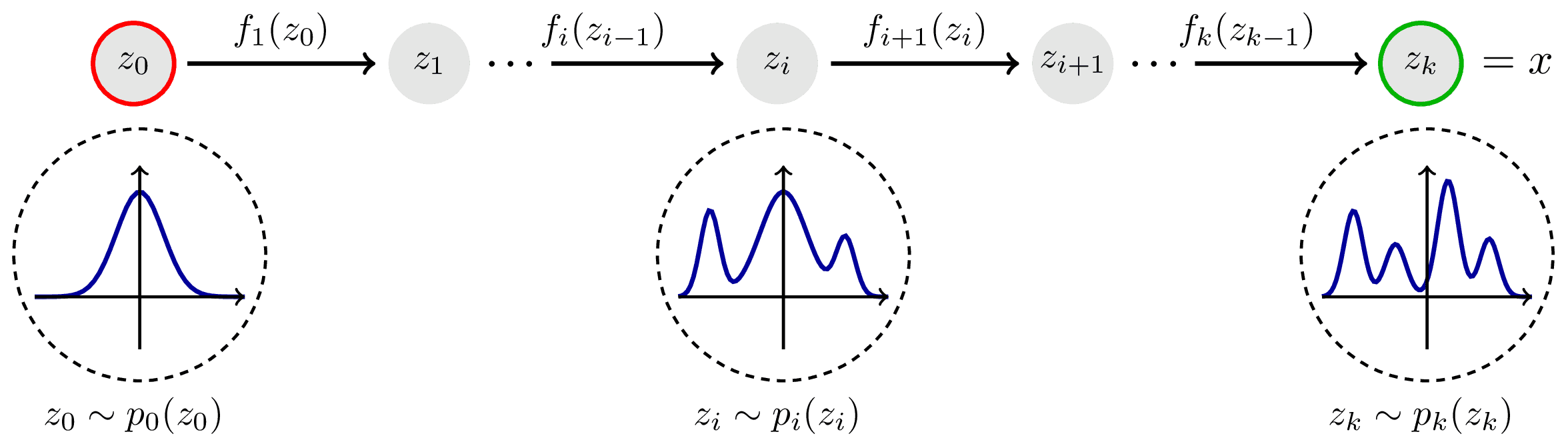
즉, transformation $\phi$ 는 다음과 같이 multiple function 의 composition 으로 표현되고, $$ \phi = \phi_{(T-1)\cdot \triangle t} \ \circ \dots \circ \phi_{1 \cdot \triangle t} \circ \phi_{0 \cdot \triangle t} $$ 각 function 에는 다음과 같은 관계가 성립합다. $$ \phi_t(x_t) = x_t + \triangle t \cdot u_t(x_t), \ \triangle t = \frac{1}{T} $$

이제 $$ T \rightarrow \infin $$ 를 생각해보면, 샘플의 변화는 더 이상 단일 함수가 아닌, Ordinary Differentiable Equation (ODE) 으로 기술된다.

$$ \frac{dx_t}{dt} = u_t(x_t) $$

여기서 $u_t(x_t)$는 시간 $t$ 와 위치 $x_t$ 가 주어졌을 때, 해당 위치의 확률 밀도 '입자'가 어느 방향과 속도로 움직여야 하는지 정의하는 velocity vector field 이다. 이제 우리의 목표는 변환 함수 $\phi$ 대신, 이 velocity field $u_t$를 신경망으로 학습하는 것이 된다.

2.2. Likelihood of CNF

Continuous Flow 을 도입하면서 얻는 가장 극적인 이점은 likelihood 계산 방식의 근본적인 변화이다. 기존의 이산적 변환에서는 계산이 거의 불가능했던 Jacobian determinant 이, 연속적인 흐름에서는 훨씬 다루기 쉬운 divergence 의 적분 으로 대체된다.

이 원리를 이해하기 위해, 먼저 확률을 하나의 'fluid' 로 바라보는 관점 에서 시작해보자.

2.2.1. Probability Fluid and Flow

시간에 따라 변화하는 어떠한 확률 분포 $p_t(x)$ 를 상상해보자.

이는 공간에 퍼져있는 수많은 미세한 'probability particle' 들의 density distribution 로도 생각할 수 있다 (입자들이 움직이면 특정 지역의 밀도는 높아지고 다른 지역은 낮아질 것). 이제 이 관점에서 몇 가지 용어를 먼저 짚고 넘어가겠다.

Probability Current:

이 probability particle 들의 움직임을 나타내는 것이 바로 velocity vector field $u_t(x_t)$ 이다. 하지만 단순히 속도만으로는 '흐름의 양' 을 알 수 없다.
밀도가 0 인 곳에서는 속도가 아무리 빨라도 흐르는 입자가 없으며, 특정 지점 $x$ 에서의 실제 '확률의 흐름의 양' 은 density $p_t(x)$와 velocity $u_t(x)$의 곱 으로 정의하는 것이 자연스럽다. 이를 Probability Current $$ J_t(x) = p_t(x) u_t(x) $$ 라고 부르며, 이 벡터는 해당 지점에서 확률이 어느 방향으로 얼마나 많이 흐르고 있는지를 나타낸다.

Net Outflow:

어떤 infinitesimal volume (미소 부피) 를 생각해보자. 이 부피 안의 probability density 가 시간에 따라 변하는 이유 ($\partial p_t / \partial t$) 는 단 하나, 경계를 통해 확률이 들어오거나 나갔기 때문이다.
이 '들어오고 나가는 양의 차이', 즉 net outflow 을 수학적으로 표현하는 도구가 바로 Divergence $\nabla$ 이다.
Divergence 은 특정 지점에서 vector field (여기서는 probability flow $J_t$) 이 얼마나 '뻗어 나오는지 (source)' 혹은 '사라지는지 (sink)'를 측정하는 값이다.
- $\nabla \cdot J_t > 0$: 해당 지점에서 확률이 밖으로 나오고 있음 ( → density 감소).
- $\nabla \cdot J_t < 0$: 해당 지점으로 확률이 들어가고 있음 ( → density 증가).
수학적으로는 각 방향의 편미분의 합으로 정의된다. $$ \nabla \cdot u_t = \frac{\partial u_1}{\partial x_1} + \frac{\partial u_2}{\partial x_2} + \dots + \frac{\partial u_D}{\partial x_D} = \sum_{i=1}^D \frac{\partial u_i}{\partial x_i} $$

따라서, 한 지점에서의 density 변화율은 Net Outflow 에 음수 부호를 붙인 것과 같으며, 이를 수식으로 나타낸 것이 바로 Continuity Equation (연속 방정식) 이다.

$$ \boxed{\frac{\partial p_t(x)}{\partial t} = - \nabla \cdot J_t(x) = - \nabla \cdot (p_t(x) u_t(x))} $$

이 방정식은 "확률은 갑자기 생기거나 사라지지 않고, 오직 흐름을 통해서만 그 밀도가 변한다" 는 확률 질량 보존 법칙을 수학적으로 표현한 것이다.

Deterministic drift (ODE) 와 더불어, 브라운 운동 같은 무작위적인 노이즈 (diffusion) 을 고려하는 일반적인 편미분 방정식이 Fokker-Planck Equation 로 알려져 있는데,

$$ \frac{\partial p_t(x)}{\partial t} = \underbrace{-\nabla \cdot [f(x,t)p_t(x)]}_{\text{Drift (flow)}} + \underbrace{\frac{1}{2}\sum_{i,j} \frac{\partial^2}{\partial x_i \partial x_j} [[g(t)g(t)^T]_{ij} p_t(x)]}_{\text{Diffusion}} $$

Continuous Normalizing Flow (CNF)는 diffusion 항이 없는 ($g=0$), 순수한 deterministic 형태이므로, CNF 가 따르는 확률 분포의 dynamics 은 Fokker-Planck Equation 의 특수한 경우인 Continuity Equation 라고도 볼 수 있다.

2.2.2. Derivation of Log-Likelihood

이제 우리는 한 입자를 따라 움직이면서 그 입자가 느끼는 log probability 의 변화율, 즉 $ \frac{d}{dt} \log p_t(x_t) $ 를 계산해야 한다.

이는 두 가지 효과의 합으로 나타낼 수 있는데,

시간이 흘러 분포 자체가 변하는 효과 (Eulerian 관점): 내가 가만히 있어도 ($x$ 고정) 시간이 흐름에 따라 변하는 내 위치의 density $$ \frac{\partial}{\partial t} \log p_t $$
내가 움직여서 다른 밀도의 지역으로 가는 효과 (Lagrangian 관점): 내가 속도 $u_t$로 움직이면서 density 가 다른 곳으로 이동하기 때문에 변하는 density
$$ \frac{dx_t}{dt} \cdot \nabla \log p_t $$

의 둘을 합친 Total Derivative 로 나타낼 수 있다. $$ \frac{d \log p_t(x_t)}{dt} = \frac{\partial \log p_t(x_t)}{\partial t} + \frac{dx_t}{dt} \cdot \nabla_x \log p_t(x_t) $$

여기서 ${dx_t}/{dt} = u_t(x_t)$ 이므로, 우리는 다음을 얻는다.

$$ \frac{d \log p_t(x_t)}{dt} = \frac{\partial \log p_t(x_t)}{\partial t} + u_t(x_t) \cdot \nabla_x \log p_t(x_t) \quad \cdots \text{(eqn. 1)} $$

i. First Term

이제 첫 번째 항인 $\partial \log p_t / \partial t$ 를 살펴보면 $$\frac{\partial \log p_t}{\partial t} = \frac{1}{p_t} \frac{\partial p_t}{\partial t} $$ 임을 알 수 있다 (로그 미분),

여기서 $\partial p_t / \partial t$ 이 위에서 살펴본 continuity equation 인 것이 보이는가? 따라서 continuity equation 을 여기에 대입하면 우리는 $$\frac{\partial \log p_t}{\partial t} = -\frac{1}{p_t} \nabla \cdot (p_t u_t) $$ 의 관계를 얻는다.

이제 divergence 의 곱셈을 다음과 같이 분배한 후, $$\nabla \cdot (p_t u_t) = (\nabla p_t) \cdot u_t + p_t (\nabla \cdot u_t) $$ 아래와 같은 결과를 얻을 수 있다. $$\frac{\partial \log p_t}{\partial t} = -\frac{1}{p_t} [(\nabla p_t) \cdot u_t + p_t (\nabla \cdot u_t)] = - \left( \frac{1}{p_t} \nabla p_t \right) \cdot u_t - (\nabla \cdot u_t) $$

이제 $\nabla \log p_t = \nabla p_t / p_t$ (score function) 관계를 이용하면, $$\frac{\partial \log p_t}{\partial t} = -(\nabla \log p_t) \cdot u_t - (\nabla \cdot u_t) \quad \cdots \text{(eqn. 2)} $$ 첫번째 항은 위와 같이 정리된다.

ii. Final Equation

이제 마지막으로, eqn1 에, $$ \frac{d \log p_t(x_t)}{dt} = \frac{\partial \log p_t(x_t)}{\partial t} + u_t(x_t) \cdot \nabla_x \log p_t(x_t) \quad \cdots \text{(eqn. 1)} $$

방금 얻은 결과인 eqn2 를 대입해보자.

$$ \begin{aligned} \frac{d \log p_t(x_t)}{dt} &= \underbrace{\left[-(\nabla \log p_t) \cdot u_t - (\nabla \cdot u_t)\right]}_{\text{from (eqn. 2)}} + u_t \cdot \nabla \log p_t \\ &= - \nabla \cdot u_t(x_t) \end{aligned} $$

결과적으로 우리는 다음과 같은 매우 간결한 최종 eqn 을 얻게 되었다.

$$ \frac{d \log p_t(x_t)}{dt} = - \nabla \cdot u_t(x_t) $$

2.2.3. Divergence & Trace

이 결과가 혁신적인 이유는 divergence $\nabla \cdot u_t$ 가 velocity field $u_t$의 **Jacobian Matrix 의 대각합 (trace)**과 같기 때문이다.

$$ \nabla \cdot u_t = \sum_{i=1}^D \frac{\partial u_{t,i}}{\partial x_i} = \text{Tr}\left( \frac{\partial u_t}{\partial x_t} \right) $$

Divergence 와 Jacobian 의 정의를 다시 살펴보면 이것이 자명하다.

Divergence: $$ \nabla \cdot u_t = \frac{\partial u_1}{\partial x_1} + \frac{\partial u_2}{\partial x_2} + \dots + \frac{\partial u_D}{\partial x_D} = \sum_{i=1}^D \frac{\partial u_i}{\partial x_i} $$
Jacobian:

$$ J_u = \frac{\partial u}{\partial x} = \begin{pmatrix} \frac{\partial u_1}{\partial x_1} & \frac{\partial u_1}{\partial x_2} & \cdots & \frac{\partial u_1}{\partial x_D} \\ \frac{\partial u_2}{\partial x_1} & \frac{\partial u_2}{\partial x_2} & \cdots & \frac{\partial u_2}{\partial x_D} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial u_D}{\partial x_1} & \frac{\partial u_D}{\partial x_2} & \cdots & \frac{\partial u_D}{\partial x_D} \end{pmatrix} $$

즉 여기서 Jacobian matrix 의 trace 를 구해보면, $$ \text{Tr}(J_u) = \frac{\partial u_1}{\partial x_1} + \frac{\partial u_2}{\partial x_2} + \dots + \frac{\partial u_D}{\partial x_D} $$ divergence 의 정의와 동일한 것을 알 수 있다.

직관적으로도 당연한 결과인데, off-diagonal 원소 $({\partial u_i}/{\partial x_j}$ , $i \neq j)$ 의 의미를 살펴보면, 이는 $j$ 축 방향으로 움직일 때 $i$ 방향 속도가 어떻게 변하는지를 나타내는 값이다.

즉, 유체의 부피 변화 (팽창/수축) 가 아닌, rotation 이나 shear 을 유발한다. 애초에 우리가 determinant 로 구하고 싶은 것은 선형 변환 간의 부피의 변화율 이었으므로 이러한 off-diagonal 들은 여기에 기여하지 않는다는 것을 알 수 있다.

결론적으로, 이산적 변환에서 필요했던 Jacobian determinant 계산이 continuous flow 에서는 Jacobian trace 계산으로 바뀌었다. Determinant 은 모든 원소에 의존하며 계산량이 $\mathcal{O}(D^3)$이지만, trace 은 대각 원소들만의 합이므로 계산이 훨씬 간단하다.

3. Flow Matching

Continuous Normalizing Flow (CNF)는 Jacobian determinant 을 trace 의 적분으로 대체하여 계산을 용이하게 만들었지만, 여전히 심각한 문제, 바로 느린 학습 속도 가 남아있다. Log-likelihood 를 계산하기 위해서는 매 학습 단계마다 ODE 를 풀어야 했고, 이는 본질적으로 diffusion model 의 느린 샘플링 과정을 매번 반복하는 것과 유사했다.

Neural Network 로 velocity field $v_\theta(x_t, t)$ 를 학습시키기 위한 이상적인 loss function 은 다음과 같다.

$$ \mathcal{L} = \mathbb{E}_{t \sim \mathcal{U}, x_t \sim p_t} [\|v_\theta(x_t, t) - u_t(x_t)\|^2] $$

이 loss function 은 시간 $t$의 샘플 $x_t$ 를 보고, 그 지점에서의 실제 속도장 $u_t(x_t)$ 를 예측하는 regression 문제이다.

$v_\theta(x_t, t)$: 우리가 학습시킬 Network 가 예측한 velocity vector field
$u_t(x_t)$: 우리가 알아야 할 'GT' marginal vector field

이는 구조적으로 DDPM 의 GT noise regression 문제와도 유사 하지만, 결정적인 차이가 존재한다. "전체 데이터 분포 $p_0$ 를 $p_1$ 으로 변환하는 'GT' marginal velocity field $u_t(x_t)$ 를 애초에 알지 못한다"는 사실이다.

이 velocity field 는 시간 $t$ 에서의 전체 데이터 분포 $p_t(x)$ 의 변화를 나타내는 복잡한 양으로, 직접 계산하는 것이 불가능하다.

3.1. Conditional Flow Matching

이 막다른 길을 뚫기 위해 Conditional Flow Matching, (CFM) 라는 트릭이 등장한다. CFM 의 핵심 아이디어는 다음과 같이 요약된다.

*"분포 전체의 경로 $p_t(x)$를 따라가는 복잡한 'marginal vector field' $u_t(x)$를 직접 학습하는 대신, 개별 샘플 쌍 ($z_0$, $z_1$)을 잇는 간단한 'conditional vector field' $u_t(x|z_1)$을 모방하도록 Network 를 학습시키자."*

이것이 어떻게 가능한지 단계별로 살펴보자.

3.1.1. Conditional Probability Path

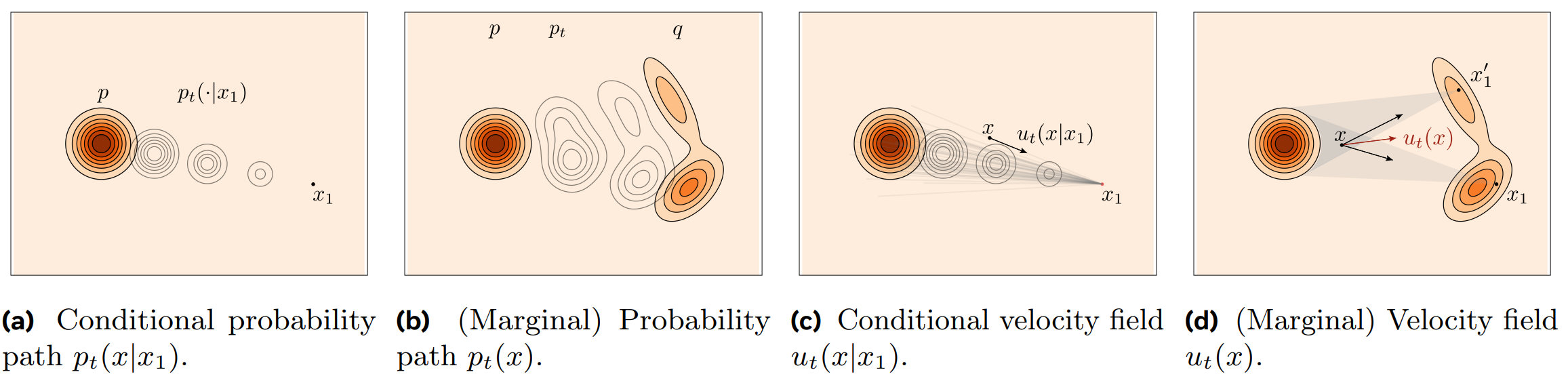
전체 분포의 알 수 없는 경로 $p_t(x)$ 대신, 다루기 쉬운 Conditional Probability Path $p_t(x|x_1)$ 를 직접 정의할 수 있을 것이다. 이는 데이터 샘플 $x_1$이 주어졌을 때, 시간 $t$ 에 입자가 어디에 있을지에 대한 확률 분포이다.

가장 대표적인 방법은 경로를 gaussian distribution 의 trajectory 으로 정의하는 것인데, $$ p_t(x|x_1) = \mathcal{N}(x | \mu_t(x_1), \sigma_t^2(x_1)I) $$ 시간 $t=0$ 에서는 standard normal distribution (완전한 노이즈) 가 되고, 시간 $t=1$ 에서는 target data $x_1$ 에 도달하도록 경계 조건을 설정하면된다.

$t=0$: $\mu_0(x_1) = 0, \sigma_0(x_1) = 1$
$t=1$: $\mu_1(x_1) = x_1, \sigma_1(x_1) = \sigma_{min} \approx 0$

이는 diffusion 의 Forward Process $q(x_t|x_0)$ 와 정확히 같은 개념적 구조를 가진다. DDPM 이 $x_0$ 에서 noise 로 가는 경로를 정의했다면, CFM 은 반대로 target $x_1$을 고정하고 그곳으로 향하는 가상의 경로를 정의하는 것이라고 해석할 수 있다.

이제 우리는 직접 설계한 path $p_t(x|x_1)$ 으로부터, 이 path 를 생성하는 conditional vector fields $u_t(x|x_1)$ 역시 continuity equation 을 통해 유도할 수 있다.

$$ {\frac{\partial p_t(x_t)}{\partial t} = - \nabla \cdot (p_t(x_t) u_t(x_t))} $$

위의 continuity equation 으로부터 아래와 같은 conditional vector fields 가 유도된다.

$$ {\frac{\partial p_t(x_t | x_1)}{\partial t} = - \nabla \cdot (p_{t|1}(x_t | x_1) u_t(x_t | x_1))} $$

_이 때, 주어진 conditional probability 를 만족하는 무수히 많은 conditional vector fields 가 존재함을 기억하자. _

path 1	path 2

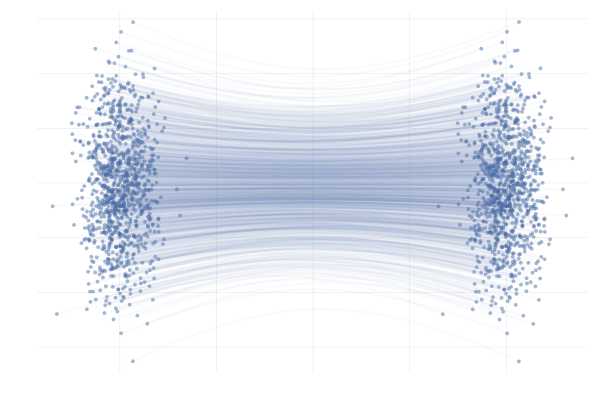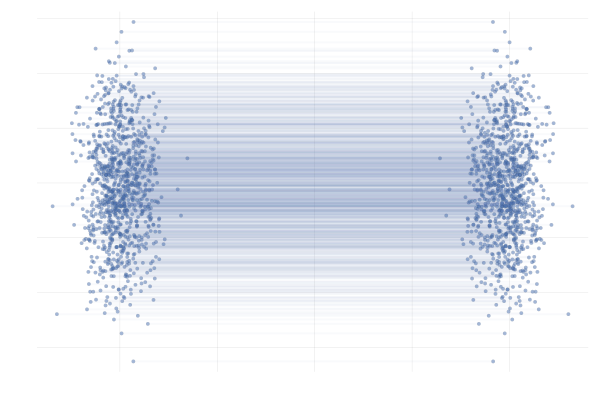3.1.2. Conditional Flow Matching

이제 CFM의 핵심인 두 가지 중요한 수학적 사실을 살펴보자.

[1] Marginal vector fields 은 conditional vector fields 의 기댓값과 같다.

marginal vector fields $u_t(x_t)$ 는 conditional vector fields $u_t(x_t|x_1)$ 을 통해 다음과 같이 나타낼 수 있고 (bayes rule), $$ u_t(x_t) = \int u_t(x_t|x_1) \frac{p_{t|1}(x_t | x_1) p_1 (x_1)}{p_t(x_t)} dx_1 $$

앞서 살펴본 continuity equation $$ {\frac{\partial p_t(x_t | x_1)}{\partial t} = - \nabla \cdot (p_{t|1}(x_t | x_1) u_t(x_t | x_1))} $$ 또한 bayes rule 을 이용해 정리해보면,

$$ \begin{aligned} \frac{\partial p_t(x_t)}{\partial t} &= \boxed{\frac{\partial}{\partial t} \int p_{t|1}(x_t | x_1)} \ p_1 (x_1) dx_1 \\ &= \boxed{ - \int \nabla \cdot (p_{t|1}(x_t | x_1) u_t(x_t | x_1)) }\ p_1 (x_1) dx_1 \\ &= - \nabla \cdot \left ( \boxed{ \int u_t(x_t | x_1)) \frac{p_{t|1}(x_t | x_1) p_1 (x_1)}{p_t(x_t)} dx_1 } \ p_t(x_t) \right ) \\ &= - \nabla \cdot \bigg [ \boxed{u_t(x_t)} \ p_{t}(x_t ) \bigg ] \end{aligned} $$

가 성립하는 것을 알 수 있다.

즉, 어떤 지점 $x_t$에서의 marginal vector fields $u_t(x_t)$ 는, 그 지점을 통과하는 모든 가능한 conditional vector fields $u_t(x_t|x_1)$ 을 평균낸 것과 같다. $$ u_t(x_t) = \mathbb{E}_{p(x_1|x_t)}[u_t(x_t|x_1)] = \int u_t(x_t|x_1) p(x_1|x_t) dx_1 $$

[2] 따라서, 전체 loss function 은 conditional loss function 과 동등하다.

첫 번째 사실로부터, 우리가 풀고 싶었던 이상적이지만 계산 불가능한 loss function 이, 계산 가능한 conditional loss function 과 동등하다는 것이 증명된다.

$$ \mathcal{L}_{\text{marginal}} = \mathbb{E}_{t, x_t} [\|v_\theta - u_t\|^2] \\ \iff \\ \mathcal{L}_{\text{CFM}} = \mathbb{E}_{t, x_1, x_t|x_1} [\|v_\theta - u_t(\cdot|x_1)\|^2] + C $$

두 loss 가 동등한 이유는 loss function 을 전개했을 때 나타나는 inner product 항을 살펴보면 명확해진다.

$$ \begin{aligned} \mathbb{E}_{x_t \sim p_t} [\langle v_\theta(x_t), u_t(x_t) \rangle] &= \int \left[ v_\theta(x_t) \cdot \boxed{u_t(x_t)} \ \right ]p_t(x_t) dx_t \\ &= \int \left[ v_\theta(x_t) \cdot \boxed{\int u_t(x_t|x_1) p_t(x_1|x_t) dx_1 } \right ]p_t(x_t) dx_t \\ &= \iint v_\theta(x_t) \cdot u_t(x_t|x_1) \boxed{ p_t(x_1|x_t) p_t(x_t)} dx_1 dx_t \\ &= \iint v_\theta(x_t) \cdot u_t(x_t|x_1) \boxed{p(x_1, x_t)} dx_1 dx_t \\ &= \mathbb{E}_{(x_1, x_t) \sim p(x_1, x_t)} [\langle v_\theta(x_t), u_t(x_t|x_1) \rangle] \end{aligned} $$

이는 알 수 없는 $u_t$에 대한 regression problem 을, 우리가 직접 설계하여 정답을 알고 있는 $u_t(\cdot|x_1)$에 대한 regression problem 로 완벽하게 대체할 수 있음을 의미한다.

3.1.3. Sampling w/ Conditional Flow

이제 마지막으로, 학습 데이터 $x_t \sim p_t(x|x_1)$는 어떻게 샘플링할까 고민해보자.

Gaussian Distribution 등에서 직접 샘플링하는 대신, CFM 은 더 효율적인 Conditional Flow Map $\phi_t$ 을 사용한다.

$$ x_t = \phi_t(x_0|x_1) = \sigma_t(x_1)x_0 + \mu_t(x_1) $$

이는 standard normal distribution (base distribution, $p_0$)에서 샘플링한 노이즈 $x_0$ 를 시간 $t$의 target distribution $p_t(x|x_1)$ 위의 한 점 $x_t$ 로 deterministic 하게 매핑하는 함수이다.

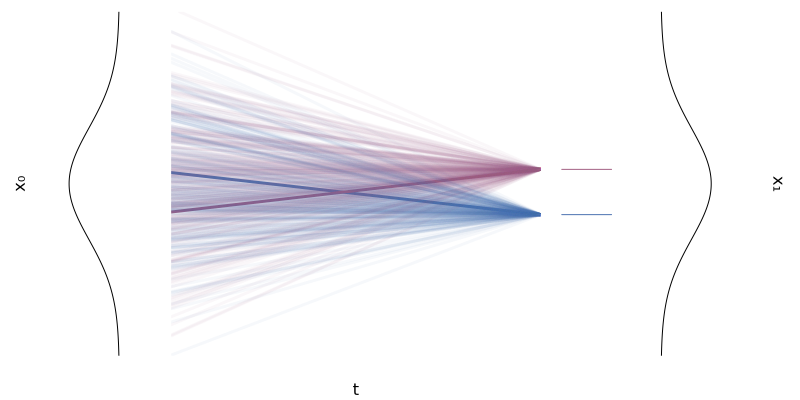
이 덕분에 우리는 복잡한 분포에서 샘플링할 필요 없이, 간단한 덧셈과 곱셈만으로 학습에 필요한 데이터 $x_t$를 생성할 수 있다.

3.2. Final Training Algorithm

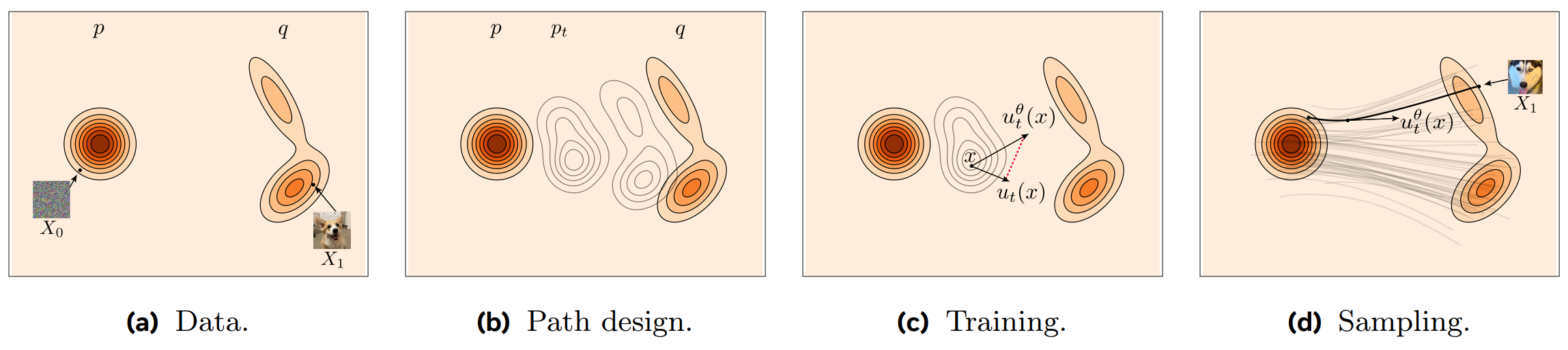
이 모든 과정을 종합하면, 최종 학습 알고리즘은 다음과 같이 단순해진다.

Sampling: base distribution 에서 노이즈 $x_0 \sim p_0$ 를, 실제 data distribution 에서 $x_1 \sim p_1$를 각각 샘플링한다.
Time Sampling: 시간 $t \sim \mathcal{U}$ 를 균등하게 샘플링한다.
Trajectory Path: Conditional Flow Map 을 이용해 경로 위의 점 $x_t = \phi_t(x_0|x_1)$ 를 계산한다.
Target Velocity: 해당 경로의 '정답' velocity $u_t(x_t|x_0, x_1)$ 를 계산한다.
Training: Neural Network $v_\theta(x_t, t)$ 가 target velocity 를 예측하도록 다음 loss 를 최소화한다: $ \mathcal{L} = |v_\theta(x_t, t) - u_t(x_t|x_0, x_1)|^2 $

결론적으로 Flow Matching 은 학습 과정에서 ODE 를 풀 필요가 전혀 없으며, 두 점을 잇는 path 의 기울기를 예측하는 간단한 regression 문제로 변환된다.

이 '두 점을 잇는 deterministic path' 라는 아이디어는 DDIM 의 핵심 통찰과도 맞닿아 있으며, Flow Matching 은 이를 학습 패러다임 자체에 녹여내어 생성 모델의 학습 효율성을 극적으로 끌어올렸다.

3.3. Rectified Flow

CFM 의 틀 안에서, 우리는 어떤 'Conditional Path' 든 자유롭게 설계할 수 있다. 여기서 Rectified Flow는 가장 단순하고 직관적인 선택을 한다.

*"노이즈 $x_0$ 와 데이터 $x_1$ 사이를 잇는 가장 간단한 경로는 직선이다."*

이 직선 경로는 확률적으로 $$ p_t(x_t|x_0, x_1) = \delta(x_t - ((1-t)x_0 + tx_1)) $$ 로 표현되며, 샘플링 관점에서는 다음과 같다.

경로: $x_t = (1-t)x_0 + t x_1$
속도: 이 경로를 만들기 위한 속도는 경로의 시작과 끝에만 의존하는 상수 벡터, 즉 $ u_t(x_t|x_0, x_1) = \frac{dx_t}{dt} = x_1 - x_0 $ 이다.

이제 CFM 의 loss function 에 이를 대입하면 Rectified Flow 의 최종 목표 함수가 완성된다.

$$ \mathcal{L} = \mathbb{E}_{t \sim U, x_0 \sim p_0, x_1 \sim p_1} \left[ \left\| v_\theta((1-t)x_0 + tx_1, t) - (x_1 - x_0) \right\|^2 \right] $$

신경망은 중간 지점 $x_t$를 보고, 최종 목적지에서 출발지를 뺀 방향 벡터 ($x_1 - x_0$) 를 맞추는 아주 간단한 regression 문제 를 풀게 된다. 이 단순함이 비약적인 학습 속도와 안정성을 가져온다.

마지막으로 Rectified Flow 은 또다른 장점이 존재한다.

한 번의 학습으로 얻어진 coupling $(Z_0, Z_1)$ 은 초기 노이즈와 데이터의 독립적인 coupling $(X_0, X_1)$ 보다 이미 훨씬 정돈된 (less entangled) 상태이다. 만약 우리가 이 $(Z_0, Z_1)$ 을 새로운 '데이터'로 삼아 다시 한번 Rectified Flow 를 학습시키면 어떻게 될까? Rectified Flow 연구진은 이 'Reflow' 과정을 반복할수록 샘플들의 이동 경로가 기하급수적으로 직선에 가까워짐을 보였다.

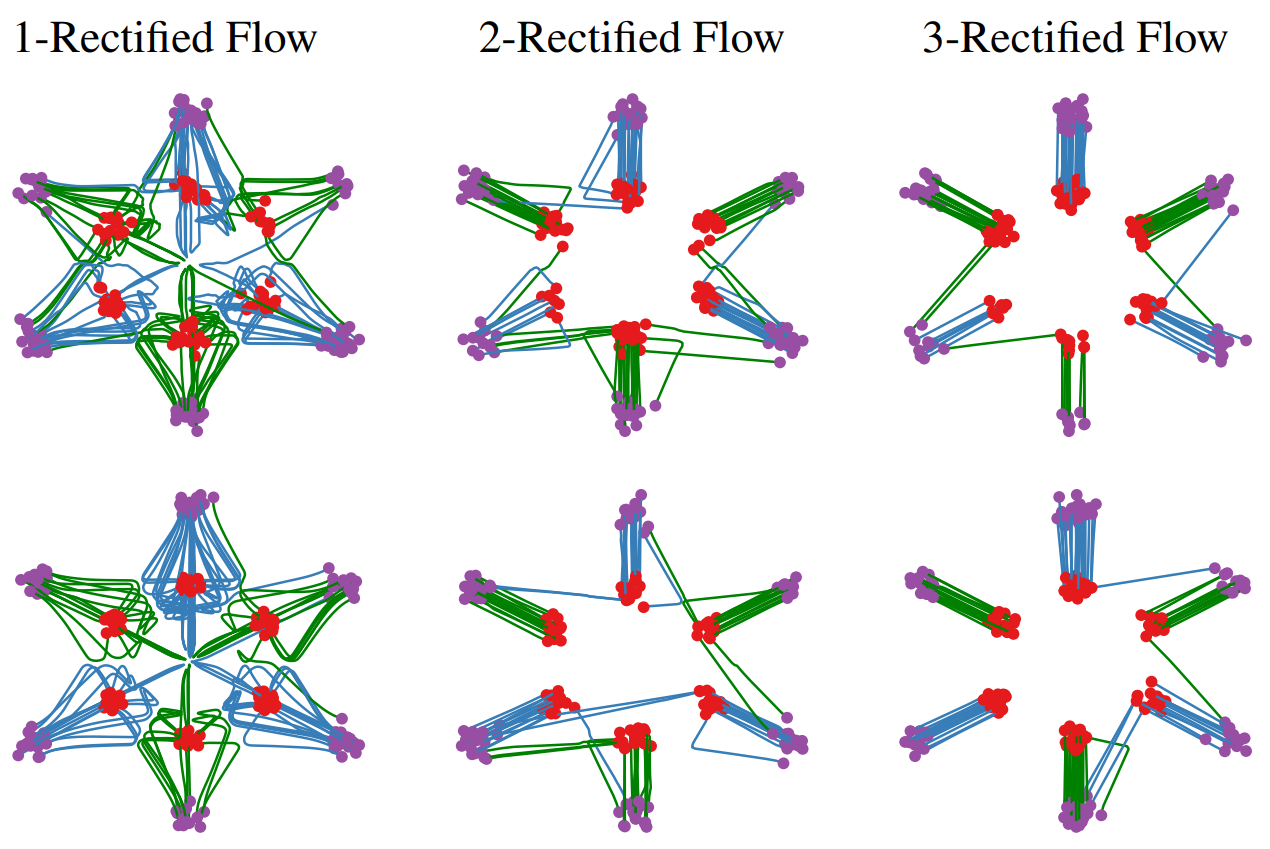
이는 단 몇 번의 반복만으로도 거의 완벽한 직선 경로를 학습할 수 있다는 의미이며, 생성 과정에서 필요한 ODE 스텝 수를 획기적으로 줄여 (심지어 단 한 스텝으로도) 매우 빠른 샘플링을 가능하게 한다.

이제 우리는 어떻게 Flow Matching을 통해 직선 경로를 학습할 수 있는지 알게 되었다. 하지만 근본적인 질문이 남는다.

"수많은 가능한 경로 중에, 왜 하필 이 '직선' 경로가 이토록 효과적인가?"

단순히 계산이 편하다는 공학적 타협일까? 아니면 그 이면에 더 깊은 수학적, 물리적 원리가 숨어있는 것일까?

Part B. Rectified Flow and Optimal Transport

앞선 질문에 답하기 위해, 우리는 하나의 가정을 설정하고, 그 가정이 어떤 결론으로 이어지는지 고찰해 보고자 한다. 바로 생성 모델이 노이즈에서 데이터로 가는 경로를 찾는 '비용 (Cost)' 을, 물리학에서 입자들이 움직이는 '총 운동 에너지 (Total Kinetic Energy)' 와 동일하다고 가정 하는 것이다.

이는 수학적으로 두 분포 사이의 L2 Wasserstein 거리를 최소화하는 Dynamic Optimal Transport 문제와 깊은 관련이 있는데, 이를 이해하기 위해 물리학의 Least Action Principle (최소 작용의 원리) 와 수학의 Optimal Transport 을 통해 그 근본 원리를 파헤쳐보자.

4. Optimal Transport

4.1. What is Optimal Transport

먼저 optimal transport 를 직관적으로 이해해보자. 여기 흙이 쌓여있는 언덕 ($X$, 소스 분포)이 있고, 이 흙을 모두 파내서 어딘가에 있는 구덩이 ($Y$, 타겟 분포)를 메워야 한다고 상상해보자.

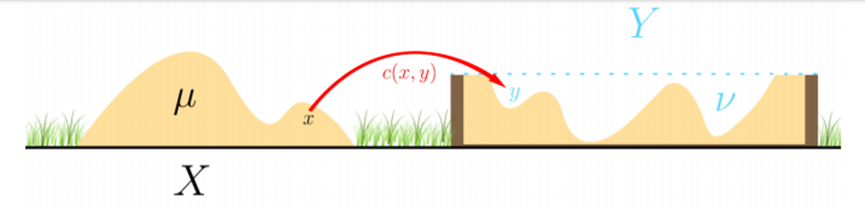
이때 "가장 효율적으로" 흙을 옮기려면 어떻게 해야 할까?

'효율적'이라는 것은 총 이동 비용(Cost)을 최소화하는 것을 의미한다. 최적 수송은 바로 이 문제, 즉 한 확률 분포 (흙더미)를 다른 확률 분포 (구덩이)로 변환하는 데 필요한 최소 비용의 Transport Plan을 찾는 수학 이론이다.

4.2. Dynamic Optimal Port

전통적인 OT는 '어디의 흙을 어디로 보낼 것인가'라는 최종 매핑 (mapping)에 집중한다. 하지만 생성 모델에서는 샘플이 점차 변해가는 경로 (path) 자체가 더 중요하며, 이는 동적 최적 수송 (Dynamic Optimal Transport) 의 영역이다. Dynamic OT에서는 시간 $t$ 에 따른 분포의 변화 $p_t$ 와 그 경로를 만드는 velocity field $v_t$ 를 고려한다.

Rectified Flow의 '직선 경로'를 단순한 수학적 트릭이 아닌, 근본적인 원리로 이해하기 위해서는 물리학의 Principle of Least Action 를 이해할 필요가 있다.

5. Classical Mechnics

5.1. What is Action

고전 역학에서, 어떤 물체가 한 지점에서 다른 지점으로 이동할 때, 가능한 수많은 경로 중에서 Action, $S$ 이라는 물리량을 최소화하는 경로를 선택하며, 이것이 바로 Principle of Least Action 이다.

이 액션은 Lagrangian, $L$ 이라는 양을 시간에 따라 적분한 값으로 정의되며,

$$ S = \int_{t_0}^{t_1} L(x, \dot{x}, t) , dt $$

라그랑지언 $L$은 그 시스템의 운동 에너지($T$)에서 위치 에너지($V$)를 뺀 값이다.

$$ L = T - V $$

유튜브 veritasium 에 action 에 대해서 정말 훌륭하게 설명하는 영상이 있으므로 참고하길 바란다: 영상 link

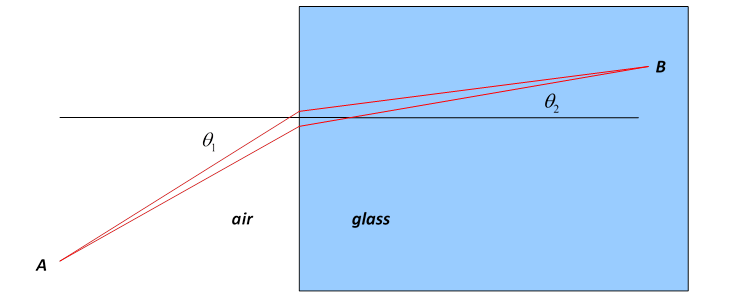
Fermat's Principle 로 알려진 빛의 굴절 현상도 (거리가 아닌 시간 최소화) Least Action Principle 의 한 예이다.

이제 가장 간단한 경우, 즉 아무런 힘 (중력, 마찰 등)이 작용하지 않는 자유 공간을 움직이는 단일 입자를 생각해보자. 이 경우 위치 에너지는 $V=0$ 이며, 라그랑지언은 순수하게 운동 에너지만 남게된다.

$$ L = T = \frac{1}{2}m v^2 = \frac{1}{2}m ||\dot{x}||^2 $$

우리는 한 분포에서 다른 분포로의 매핑 자체에만 관심이 있고, 그 과정에서 특정 경로에 패널티를 주는 외부 요인 (Potential) 을 가정하지 않으므로, 시스템의 비용은 순수하게 입자들의 이동 거리와 속도 (Kinetic Energy) 에만 의존한다고 볼 수 있다.

이 때, 이 입자의 액션은 다음과 같으며

$$ S = \int_{t_0}^{t_1} \frac{1}{2}m ||\dot{x}(t)||^2 , dt $$

최소 작용 원리에 따르면, 입자는 이 action $S$를 최소화하는 경로를 따라 움직인다. 적분 안의 값이 항상 양수이므로, 이 값을 최소화하는 가장 직관적인 방법은 속도($||\dot{x}||$)를 일정하게 유지하며 최단 거리, 즉 직선으로 움직이는 것일 것이다.

실제로 위 액션을 최소화하는 경로를 찾기 위한 미분방정식을 풀어보면, 가속도($\ddot{x}$)가 0이라는 결과가 나온다 ($m\ddot{x} = 0$). 이는 곧 등속 직선 운동을 의미한다.

5.2. Euler-Lagrange Equation

Euler-Lagrange Equation 이란, action 을 최소화 (혹은 stationary 하게, 즉, 극값이나 saddle point!) 하게 만드는 조건에 대한 미분방정식이다.

이는 변분법으로 유도할 수 있으며, 아래와 같이 정의된다:
$$ \frac{\partial L}{\partial x} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) = 0 $$

이 방정식의 각 항이 의미하는 바는 다음과 같은데,

${\partial L}/{\partial x}$ : 경로의 **위치($x$)**가 변할 때, 라그랑지언 (cost)이 얼마나 변하는가?
${\partial L}/{\partial \dot{x}}$ : 경로의 **속도($\dot{x}$)**가 변할 때, 라그랑지언 (cost)이 얼마나 변하는가? (참고: 이 값은 운동량 $p=mv$와 같다)
${d}/{dt}(\dots)$ : 변화량이 시간에 따라 어떻게 변하는가?

즉, 위 방정식을 품으로써 우리는 action 을 최소화하는 조건의 해가 무엇인지를 구할 수 있다. 이제 우리가 1단계에서 구한 라그랑지언 $L = \frac{1}{2}m\dot{x}^2$ 을 이 방정식에 넣고 계산해 보자.

첫 번째 항: ${\partial L}/{\partial x}$ 계산

라그랑지언 $L = \frac{1}{2}m\dot{x}^2$ 을 보자. 이 식에는 위치를 나타내는 변수 $x$가 없으며, 오직 속도 $\dot{x}$ 만 들어있다. 따라서, 위치 $x$에 대해 미분하면 그 값은 0 이 된다.

$$ \frac{\partial L}{\partial x} = \frac{\partial}{\partial x}\left(\frac{1}{2}m\dot{x}^2\right) = 0 $$

직관적으로는 자유 공간에서는 입자가 어디에 있든 비용(라그랑지언)은 동일하다고 볼 수 있다. 비용은 오직 얼마나 빠른지 에만 의존하기 때문.

두 번째 항: $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right)$ 계산 먼저 ${\partial L}/{\partial \dot{x}}$ 부터 살펴보자. 라그랑지언 $L = \frac{1}{2}m\dot{x}^2$ 을 속도 $\dot{x}$에 대해 미분하면,

$$ \frac{\partial L}{\partial \dot{x}} = \frac{\partial}{\partial \dot{x}}\left(\frac{1}{2}m\dot{x}^2\right) = \frac{1}{2}m(2\dot{x}) = m\dot{x} $$

이 되고, 이 결과를 시간 $t$에 대해 다시 미분하면,

$$ \frac{d}{dt}\left(m\dot{x}\right) $$

질량 $m$은 상수이므로 밖으로 나오고, 속도 $\dot{x}$를 시간으로 미분하면 가속도 $\ddot{x}$가 된다.

$$ \frac{d}{dt}\left(m\dot{x}\right) = m \ddot{x} $$

이제 두 결과를 대입해보면, $$ \frac{\partial L}{\partial x} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot{x}}\right) = 0 $$ $$ 0 - m\ddot{x} = 0 $$ 질량 $m$ 은 0이 아니므로, 이 식이 성립하려면 반드시 다음 조건이 만족되어야 하는 것을 알 수 있다.

$$ \ddot{x} = 0 $$

즉 이는 가속도가 0인, 등속 직선 운동(uniform linear motion) 을 의미하게 된다.

5.3. Action in Optimal Transport

5.3.1. Action in Probability Distribution

이제 이 개념을 단일 입자에서 무수히 많은 입자들의 집합, 즉 확률 분포로 확장해 보자.

단일 입자의 운동 에너지: $T = \frac{1}{2}m ||v||^2$
확률 분포의 총 운동 에너지: 분포를 구성하는 모든 입자들의 운동 에너지의 기댓값

시간 $t$에서의 분포를 $p_t(x)$로, 각 지점 $x$에서의 입자들의 속도를 속도장 $v_t(x)$로 표현한다. 특정 시간 $t$에서의 총 운동 에너지는 각 지점의 운동 에너지($\frac{1}{2}||v_t(x)||^2$)를 그 지점의 밀도($p_t(x)$)로 가중 평균하여 계산할 수 있다.

$$ \text{Total Kinetic Energy at } t = \mathbb{E}_{x \sim p_t}\left[\frac{1}{2}||v_t(x)||^2\right] = \int \frac{1}{2}||v_t(x)||^2 p_t(x) ,dx $$

자유 입자와 마찬가지로, 외부 힘이 없는 분포의 변환 (위치 에너지가 없는 경우) 을 가정하면 이 시스템의 라그랑지언은 총 운동 에너지가 된다. 따라서 전체 변환 과정의 액션은 이 총 운동 에너지를 시간에 대해 적분한 값이 된다.

$$ \mathcal{A}(p_t, v_t) = \int_0^1 \left( \int \frac{1}{2}||v_t(x)||^2 p_t(x) ,dx \right) dt $$

최소 작용의 원리와 같이, 우리는 이 액션을 최소화하는 경로 ($p_t, v_t$) 를 찾고자 한다.

이렇게 확률 분포의 변환을 총 운동 에너지 (Action) 를 최소화하는 경로를 찾는 문제로 재정의하는 것은 optimal transport 에서 'Benamou-Brenier formula' 로 알려진 dynamic OT 공식의 핵심 아이디어와 정확히 일치한다. 우리는 지금 생성 모델의 문제를 유체 역학의 언어로 풀어내고 있는 셈이다.

5.3.2. Constrained Euler-Lagrange Equation

여기서도 한 가지 제약 조건이 있다. Flow 절에서 살펴봤던 continuity equation 이 기억나는가? 이는 입자 (probability mass)는 갑자기 생기거나 사라지지 않고 보존되어야 하는 확률 질량 보존을 나타내는 식이었다.

우리는 probability distribution 에 대한 문제를 풀고 있으므로, 여기서는 continuity equation 이 우리가 지켜야하는 constraint 가 된다.

$$ \frac{\partial p_t}{\partial t} =- \nabla \cdot (p_t v_t) $$

이러한 제약이 있는 최적화 문제를 풀기 위해, Lagrange Multiplier 함수 $\phi(x, t)$ 를 도입한다. 이 함수는 액션에 제약 조건을 결합하여 새로운 functional $\mathcal{L}$을 만든다.

$$ \mathcal{L}[p, v, \phi] = \mathcal{A}[p, v] - \int_0^1 \int_{\mathbb{R}^d} \phi(x, t) \left( \frac{\partial p_t}{\partial t} + \nabla \cdot (p_t v_t) \right) ,dx ,dt $$

이제 제약 조건 없는 $\mathcal{L}$ 을 최적화하는 문제로 바꿀 수 있다. 최적의 경로에서 $\mathcal{L}$ 은 $p$, $v$, $\phi$ 의 미소 변화 (variation) 에 대해 안정적이어야 한다. 즉, 각 변수에 대한 functional derivative 이 0이 되어야 한다.

계산을 용이하게 하기 위해, 제약 조건 항에 부분적분 (integration by parts)을 적용하여 미분을 $p$ 와 $v$ 에서 $\phi$ 로 옮겨보자.

$$ \mathcal{L} = \int_0^1 \int_{\mathbb{R}^d} \left( \frac{1}{2} |v|^2 p + p \frac{\partial \phi}{\partial t} + p v \cdot \nabla \phi \right) dx dt - \int_{\mathbb{R}^d} [\phi p]_0^1 dx $$

이제 이 식을 이용하여 각 변수에 대한 variation 을 계산한다.

Velocity $v$ 에 대한 functional derivative $\mathcal{L}$ 을 속도 $v$ 에 대해 functional derivative ($\delta_v \mathcal{L}$)하고 그 결과를 0 으로 둔다.

피적분 함수를 $v$ 에 대해 미분하면 $p v + p \nabla \phi = p(v + \nabla \phi)$ 이고, 이 값이 0 이 되려면 다음이 성립해야 한다. $$ v + \nabla \phi = 0 $$

따라서 첫 번째 핵심 결과, 즉 최적 vector field ($v_t$) 은 어떤 scalar potential function ($\phi$) 의 gradient 여야 한다는 것을 얻는다. $$ {v_t(x) = -\nabla \phi(x, t)} $$

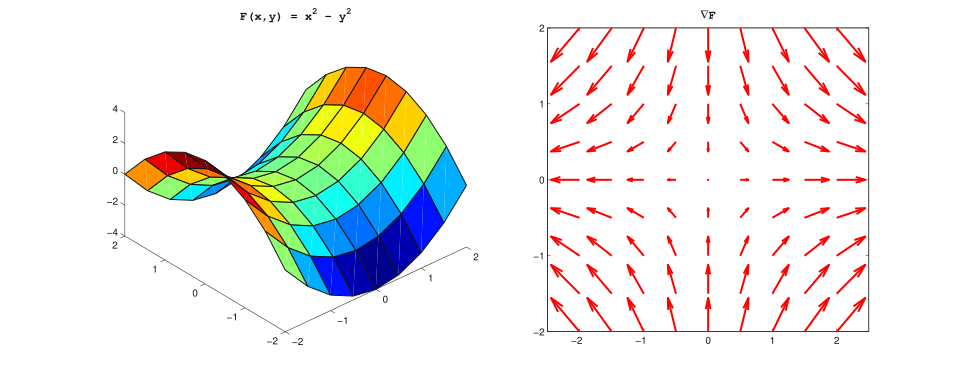- Vector field (right) and corresponding scalar potential (left).

Density $p$ 에 대한 functional derivative

이제 $\mathcal{L}$ 을 density $p$에 대해 functional derivative ($\delta_p \mathcal{L}$) 하고 그 결과를 0으로 둔다.피적분 함수는 $p$ 에 대해 선형이므로, 이 변분이 0이 되려면 괄호 안의 항이 0이 되어야 한다. $$ \frac{1}{2} |v|^2 + \frac{\partial \phi}{\partial t} + v \cdot \nabla \phi = 0 $$

Hamilton-Jacobi Equation 이제 첫 번째 결과 ($v = -\nabla \phi$) 를 두 번째 결과에 대입해보자. $$ \frac{1}{2} |-\nabla \phi|^2 + \frac{\partial \phi}{\partial t} + (-\nabla \phi) \cdot (\nabla \phi) = 0 $$

$$ \frac{1}{2} |\nabla \phi|^2 + \frac{\partial \phi}{\partial t} - |\nabla \phi|^2 = 0 $$

이를 정리하면, 포텐셜 함수 $\phi$가 만족해야 하는 편미분방정식, 즉 Hamilton-Jacobi Equation 을 얻는다. $$ {\frac{\partial \phi}{\partial t} - \frac{1}{2} |\nabla \phi(x, t)|^2 = 0} $$

이 방정식은 자유 입자의 운동을 설명하는 고전 역학의 근본적인 방정식이다.

가속도가 0 임을 증명하기 마지막으로 이 최적의 vector field 를 따라 움직이는 입자의 경로 $x(t)$를 생각해 보자. 입자의 속도는 $\dot{x}(t) = v_t(x(t))$ 이다. 우리는 이 입자의 가속도 $\ddot{x}(t)$가 0임을 보이면 된다.

가속도 $\ddot{x}(t)$는 속도 $v_t(x(t))$의 시간에 대한 total derivative 이다. $$ \ddot{x} = \frac{d}{dt} v_t(x(t)) = \frac{\partial v}{\partial t} + (v \cdot \nabla)v $$ 각 항을 포텐셜 $\phi$로 표현해 보자.

첫 번째 항: 위에서 유도한 Hamilton-Jacobi Equation ($\frac{\partial \phi}{\partial t} = \frac{1}{2}|v|^2$) 과 $v = -\nabla\phi$ 관계를 이용하면, $$ \frac{\partial v}{\partial t} = \frac{\partial}{\partial t}(-\nabla \phi) = -\nabla\left(\frac{\partial \phi}{\partial t}\right) = -\frac{1}{2}\nabla(|v|^2) $$
두 번째 항: vector field $v$는 scalar potential $\phi$ 의 gradient ($v = -\nabla\phi$) 이므로, 회전 (curl)이 0이다 ($\nabla \times v = \nabla \times (-\nabla\phi) = 0$). 따라서, $$ (v \cdot \nabla)v = \frac{1}{2}\nabla(|v|^2) $$ 이제 두 항을 조합하여 가속도를 계산하면, $$ \ddot{x} = \frac{\partial v}{\partial t} + (v \cdot \nabla)v = -\frac{1}{2}\nabla(|v|^2) + \frac{1}{2}\nabla(|v|^2) = 0 $$

cf: $$\frac{1}{2}\nabla(A \cdot A) = (A \cdot \nabla)A + A \times (\nabla \times A) $$

5.4. Why Recitifed-Flow is Linear?

$$ \ddot{x}(t) = 0 $$

Action 을 최소화하고 continuity equation 을 만족하는 최적의 흐름을 따르는 모든 입자의 가속도는 0 이다. 이는 각 입자가 시작점 $z_0$에서 도착점 $z_1$까지 등속 직선 운동을 한다는 것을 수학적으로 증명한다.

이것이 바로 Rectified Flow가 두 분포의 샘플 $z_0, z_1$을 뽑아 그 사이를 잇는 직선 경로를 학습의 목표로 삼는 강력한 이론적 배경이다. 모델이 학습하는 속도 벡터 $$v = z_1 - z_0$$는 이 최적 경로의 속도장에 해당한다.

따라서 Rectified Flow가 채택한 '직선 경로' $z_t = (1-t)z_0 + t z_1$ 는 임의의 선택이 아니라, 물리 법칙과 수학적 최적화에 근거한 가장 자연스럽고 효율적인 경로라고 해석할 수 있다.

6. Rectified Flow on Manifolf

Part B에서 우리는 최소 작용의 원리를 통해 Rectified Flow의 '직선 경로'가 물리적으로 최적의 경로임을 보였다. 자유 공간에서 Action 을 최소화하는 경로는 등속 직선 운동이라는 결론은 명쾌하고 아름답다.

하지만 여기서 의문이 하나 남는다.

"우리가 다루는 데이터가 과연 '자유 공간'에 살고 있는가?"

이미지, 음성, 단백질 구조와 같은 고차원 데이터는 단순한 유클리드 공간 (Euclidean Space, $\mathbb{R}^d$)이 아닌, 그 안에 복잡하게 휘어져 있는 Manifold 위에 존재한다고 가정하는 것이 훨씬 합리적이다. Manifold 란, 국소적으로는 Euclidean Space 의 성질을 갖는 (평면) topology 를 말한다 (평평이들이 지구를 평평하게 생각하는 이유!).

이러한 관점에서 Part B의 결론은 치명적인 한계를 가진다. 우리가 유도한 '직선 경로' 는 오직 공간이 평평하다고 가정할 때만 최적이다. 지구 표면의 두 도시를 잇는 최단 경로가 상공을 가로지르는 직선이 아니라 지구 표면을 따라가는 곡선 (대권 항로)이듯이, Manifold 위에서의 최적 경로는 더 이상 직선 이 아닐 것이다.

그렇다면 Rectified Flow의 '직선' 이라는 아이디어는 근본적인 한계에 부딪힌 것일까? 이 질문에 답하기 위해, 우리는 Part A 와 B 에서 구축한 도구들을 평평한 Euclidean Space 에서 휘어진 Riemannian Manifold 로 확장 해야 한다.

Riemannian Manifold $(M, g)$는 각 지점 $x$가 국소적으로는 Euclidean Space 처럼 보이는 공간 $M$ 과, 각 지점의 Tangent Space $T_M$ 위에서 거리와 각도를 측정하는 Riemannian Metric $g$ 로 구성된다.

이제 우리의 핵심 방정식들이 이 휘어진 공간 위에서 어떻게 변하는지 살펴보자.

6.1. Dynamics on a Manifold

Part A에서 우리는 확률 분포의 동역학이 Continuity Equation 으로 기술됨을 보았다.

Euclidean Space: $${\frac{\partial p_t(x)}{\partial t} = - \nabla \cdot (p_t(x) u_t(x))}$$

이 방정식은 Manifold 위에서도 거의 동일한 형태로 유지되며, eucllidean divergence ∇· 이 Riemannian divergence div_g 으로 대체될 뿐이다.

Riemannian Manifold: $${\frac{\partial p_t(x)}{\partial t} + \text{div}_g(p_t u_t)(x) = 0}$$

이 리만 연속 방정식 덕분에, Part A 에서 유도했던 가장 중요한 결과 중 하나인 log-likelihood의 변화율 역시 Manifold 위에서 그대로 성립한다.

$$ \frac{d}{dt} \log p_t(\psi_t(x)) = - \text{div}_g(u_t)(\psi_t(x)) $$

이는 Continuous Normalizing Flow 의 핵심 메커니즘이 데이터의 기하학적 구조가 Euclid Space 가 아니더라도 여전히 유효함을 의미한다. 우리는 여전히 velocity field u의 divergence 을 통해 log-likelihood 를 계산할 수 있다.

6.2. Flow Matching on a Manifold

이제 매칭할 목표인 Loss 함수를 재정의해야 한다.

Euclidean Space 에서는 두 벡터의 차이를 L2 norm으로 측정했다. Manifold 에서는 이 역할을 Riemannian Metric $g$가 정의하는 내적 $⟨·,·⟩_g$ 이 대신한다.

따라서, Riemannian Conditional Flow Matching (RCFM) 의 Loss 함수는 다음과 같다.

$$ \mathcal{L}_{\text{RCFM}}(\theta) = \mathbb{E}_{t, x_1, x_t|x_1} \left[ \left\| u_t(x_t|x_1) - v_\theta(x_t, t) \right\|^2_g \right] $$

여기서 $||·||^2_g$ 는 metric $g$에 의해 유도된 squared norm 으로, 두 속도 벡터 $u$ 와 $v$ 가 동일한 tangent space $T_{x_t}M$ 내에 존재할 때 그 차이를 측정한다.

L2 norm 의문에 대한 핵심적인 답변이 바로 여기에 있다. L2 norm 은 Riemannian Metric $g$ 가 Euclidean metric 인 특수한 경우일 뿐이며, Flow Matching framework 는 데이터에 더 적합한 기하학적 구조를 반영하는 어떤 metric $g$ 도 수용할 수 있다.

6.3. Geodesic Flow

마지막 질문은 이것이다: Euclidean Space 의 '직선 경로'는 Manifold 위에서 무엇으로 대체되는가? 정답은 Geodesic, 휘어진 공간 위에서 두 점을 잇는 최단 경로이다 (비행기의 최단 항로 또한 geodesic 이다).

Rectified Flow의 linear interpolation 을 다시 한번 분해해보자. $$ x_t = (1-t)x_0 + t x_1 = x_0 + t(x_1 - x_0) $$ 이 간단한 식에는 사실 세 가지 핵심적인 행동이 숨어있다.

Start $x_0$
Direction $(x_1 - x_0)$ 를 따라
Move $x_0 + t \cdot (x_1 - x_0)$ 만큼

여기서 핵심은 "점과 벡터의 덧셈" (+) 과 "점들의 뺄셈" (-) 이 너무나 자연스럽게 정의된다는 것이다. 왜냐하면 공간이 평평해서 어디에서나 방향과 거리의 개념이 동일하기 때문이다.

이제 이 개념을 휘어진 공간 Manifold space 으로 가져와보자. 예를 들고 있는 지구라는 Manifold 에서, ‘시작점: 서울’ 과 ‘도착점: 뉴욕’ 을 생각해본다면,

Direction: “뉴욕의 위치 좌표 - 서울의 위치 좌표” 는 무엇을 의미하는가? 어떤 좌표계를 쓰든 (위도나 경도의 Spherical or Euclidean Coordinates, what else!) 방향 벡터 를 의미하지는 않는다. Manifold space 에서, 좌표를 빼서 방향 벡터를 구하는 간단한 방법은 없다.
Move: (일단 어떻게든) 방향 벡터를 구했다손 치자. 서울 → 뉴욕은 어떻게 이동해야 하는가? 서울의 좌표 + 이동거리 * 방향벡터 는 과연 어디를 가리키는가? Manifold 에서는 flat 한 Euclidean space 의 ‘덧셈’ 이 통하지 않는다.

즉, 휘어진 공간에서는 "어디로 가야 하는지"와 "그 방향으로 실제로 가는 법" 을 새롭게 정의해야한다. 그리고 이를 정의한 것이 바로 Exponential Map 이다.

Logarithmic Map: 시작점 $x_0$ 에서 도착점 $x_1$ 으로 향하는 최단 경로의 '초기 속도 벡터' $v \in T_{x_0}M$를 계산한다. 이 역할을 하는 것이 로그 맵(Logarithmic Map) 이다. $$ v = \text{log}_{x_0}(x_1) $$
Exponential Map: 시작점 $x_0$에서 속도 벡터 $v$ 를 가지고 $t$만큼 geodesic 경로를 따라 이동했을 때의 도착 지점을 계산한다. 이 역할을 하는 것이 Exponential Map 이다. $$ x_t = \text{exp}_{x_0}(t \cdot v) $$

cf. 여기서 Exp / Log 의 이름은 우리가 scalar function 에서 수행하는 exp, log 연산이 아니라, linear differential equation 의 해로써의 ‘exp’, 그리고 그에 대한 invert ‘log’ 로써의 이름에 가깝다 (Lie Group ↔ Algebra 간에 사용하는 exp/log map 과 같은 개념). Manifold 위에서의 ‘뺄셈’과 ‘덧셈’의 일반화 된 정의에 가깝다고 해석하는 것이 좋다.

이제 이 두 가지를 결합하면, Manifold 위에서의 Geodesic Conditional Flow 가 완성된다.

$$ \psi_t(x_0|x_1) = \text{exp}_{x_0} (t \cdot \text{log}_{x_0}(x_1)) $$

이것이 바로 진정한 의미의 Rectified Flow 이다. 모델은 이제 Euclidean 공간의 직선이 아닌, Manifold 위의 최단 경로인 Geodesic 을 따라 흐르도록 학습된다.

이제 자유 입자의 Action 을 Manifold 위에서 재정의하면, 총 운동 에너지를 Riemannian Metric $g$ 를 이용해 계산하고 이를 시간에 대해 적분하는 형태가 된다. 그리고 이 Action 을 최소화하는 경로는, 정의에 따라, 바로 Geodesic 이다.

따라서 Rectified Flow의 '직선 경로' 라는 아이디어는 유클리드 공간에 국한된 특수한 경우가 아니었다. 그것은 "주어진 기하학적 구조 (Manifold, metric) 하에서 에너지 소모 (Action)가 가장 적은 경로를 따른다" 는 더 깊고 일반적인 물리적 원리의 한 단면을 반영한다. $$\ddot{x}=0$$ 이라는 단순한 방정식은, Manifold 위에서는 더 복잡한 geodesic equation 으로 대체되지만 그 근본 원리는 동일하다.

7. Last Dicussion: Why Linear?

Q. Rectified Flow의 미스터리: 왜 '틀린' 직선 경로가 작동하는가?

앞서 살펴본 것처럼 우리가 추구하는 가장 이상적인 변환 경로는 manifold 위에서의 최단 거리인 Geodesic 이다. 이는 유클리드 공간의 덧셈/뺄셈을 manifold의 언어인 exp/log 맵으로 일반화한 것이며, Rectified Flow의 '궁극적인' 형태라고 할 수 있다.

$$ \psi_t(x_0|x_1) = \exp_{x_0}(t \cdot \log_{x_0}(x_1)) $$

하지만 이 아름다운 이론은 고차원 이미지 데이터 앞에서 계산 불가능성이라는 현실의 벽에 부딪히게 된다. 실제 Rectified Flow 모델들은 이 모든 복잡성을 무시하고, 데이터 공간이 평평하다고 가정하는 가장 단순한 직선 경로 를 사용한다.

$$ x_t = (1-t)x_0 + t x_1 $$

이 경로는 필연적으로 데이터가 존재하는 저차원 manifold 를 벗어나 '허공'을 가로지른다. 이론적으로는 '틀린' 경로임에도, 이 '아름다운 편견'은 놀라울 잘 작동한다.

대체 왜 그럴까?

1. Vector Field as a Corrective "Gravity Well"

Rectified Flow는 단순히 두 점을 잇는 선을 배우는 것이 아니라, 공간 전체에 걸쳐 정의된 Vector Field $v_\theta(x, t)$ 를 학습한다. 이 벡터장의 진짜 임무는 다음과 같다.

"만약 어떤 입자 $x_t$ 가 manifold를 벗어난 '허공'에 놓여있다면, 그 입자를 다시 데이터가 존재하는 고밀도 영역 (manifold)으로 되돌려놓는 '평균적인 최적의 방향'을 알려주는 것."

수학적으로 이는 조건부 기댓값(Conditional Expectation)으로 표현된다. 모델은 수많은 데이터 쌍 $(X_0, X_1)$에 대한 평균 속도 를 학습한다. $$ v_\theta(x_t, t) \approx \mathbb{E}[X_1 - X_0 \mid (1-t)X_0 + tX_1 = x_t] $$ 이 '평균화' 과정을 다시 생각해본다면, 어떤 점 $x_t$ 가 manifold 에서 멀리 떨어져 있다면, 그 점을 통과하는 수많은 직선 경로들의 평균적인 방향은 자연스럽게 manifold 의 중심을 향하게 된다. 마치 질량이 큰 물체 (데이터 manifold)가 주변 공간을 휘게 하여 '중력장'을 만드는 것과 같다.

따라서 ODE 솔버가 이 벡터장을 따라 스텝을 밟아 나갈 때, 그 실제 궤적은 직선이 아니라 manifold 의 곡률을 따라가는 매끄러운 곡선 이 된다.

2. Implicit Space Straightening by Neural Networks

Transformer 와 같은 강력한 Deep Neural Network 는 입력 $x_t$ 를 있는 그대로 처리하지 않는다. 모델은 사실 두 가지 일을 동시에 수행한다.

Encoding (Unfolding): 네트워크의 초기 레이어들은 복잡하게 휘어진 데이터 manifold 를, 선형 연산이 훨씬 잘 통하는 '거의 평평한' latent feature space 으로 암묵적으로 encoding 한다.
Decoding (Folding): 모델은 이 '펴진' 공간에서 간단한 방향 벡터를 예측한 뒤, 후기 레이어들을 통해 그 결과를 다시 원래의 휘어진 공간에 맞는 벡터장으로 'decoding'하여 출력한다.

즉, 모델은 "휘어진 공간에서 직선을 억지로 따라가는 법" 을 배우는 것이 아니라, "공간을 펴서 직선을 따라간 뒤, 다시 원래대로 되돌리는 변환 자체" 를 학습한다.

3. Starting in an Explicitly Straightened Latent Space

이 아이디어는 Latent Diffusion Model (LDM)이나 Stable Diffusion 3 와 같은 최신 모델에서 그 실용성이 극대화된다. 이 모델들은 픽셀 공간에서 직접 Flow 를 학습하는 대신, 잘 학습된 VAE Latent Space 안에서 Flow 를 학습한다.

VAE latent space 는 이미지를 의미적으로 풍부하고 구조화된 공간으로 압축하도록 설계되었다. 이 공간에서는 '고양이 사진'과 '개 사진' 사이의 변환이 픽셀 공간에서보다 훨씬 더 선형적이고 부드러운 경로를 가질 가능성이 높다.

따라서 우리의 가정은 "수백만 차원의 이미지 공간이 평평하다"는 강한 가정이 아니라, "VAE가 학습한 수천 차원의 '개념의 공간'이 (상대적으로) 평평하다" 는 훨씬 더 약하고 합리적인 가정으로 바뀌게 된다. 이는 Rectified Flow 가 놀라운 성능을 내는 가장 실용적인 이유 중 하나이다.

마치며

여기까지 긴 글을 읽어주셔서 감사합니다.

사실 이 글은 요새 집필 중인 시리즈 글 : Building Large 3D Generative Model from Scratch 에서 Model Structure 를 설명하는 부분에서 시작하였습니다.

Flow 는 최근 이미지, 비디오 뿐만 아니라 3D 생성에서도 Network 를 훈련시키는 dominant framework 이기 때문에 flow 에 대한 제반 사항을 명료하게 정리할 필요가 있었고, 그 부분이 너무 길어지는 바람에 따로 글을 분리하였습니다.

최대한 제가 아는 지식 내에서 flow 에 대한 내용을 정리해보았지만, 전공이 수학이나 물리는 아니라 action 을 비롯해 여러 개념을 전개하는 과정에서 오류가 있을 수 있습니다. 언제든 날카로운 지적과 가르침을 댓글로 남겨주시면 감사히 배우고 수정하겠습니다.

다음 글부터는 다시 Building Large 3D Generative Model from Scratch 시리즈로 돌아가서, 예고한대로 multi node 환경에서의 training 에 대해 톺아볼 예정입니다. 블로그 자체가 좀 더 이론을 잘 이해하고 설명하는데 치중한 경향이 있는데, 흔치 않게 CS 적인 글이 되겠네요.

감사합니다 :)