TL; DR
3D Gaussian Splatting 은 강력하고 매력적인 기술이지만, rasterization 을 사용하기 때문에 생기는 여러 문제가 있다. 최근 공개된 3D Gaussian Ray Tracing (이하 3D GRT) 은 Ray Tracing 기술을 3D Gaussian 에 접목시켜 이러한 단점을 많이 해결한 모습을 보여주었다. 이 글을 통해 3D GRT 를 자세하게 알아보자!
- project page: Link

1. Introduction
Challenges in 3D Gaussian Splatting
3D Gaussian Splatting 은 well-designed tile-based rasterizer 를 이용해 high-fidelity novel-view synthesis 와 real-time rendering 을 달성한 연구이다.
Next-photogramerry 로까지 불리며 각광받고 있는 연구분야지만, 아직 과도기이기 때문에 극복해야할 문제가 많이 남아있다.
그 중 대표적인 것이 바로 Rasterization 사용으로 인한 문제들이다.
-
다양한 Camera Model 에 유연하지 못하다.
이전 3D GS rasterization 분석글 에서도 지적한 바와 같이 EWA splatting 으로 구현된 rasterization 은 affine projection error 가 있으며, 이 때문에 다양한 camera 에 대한 modeling 을 구현하더라도 high-quality 로 학습하는 것이 쉽지 않다.
Inflexibility of 3D GS with Diverse Camera Models, source: Optimal GS -
Image Quality 에 민감하다.
MLP 로 이루어진 NeRF 는 image 간 calibration 차이에도 일부 강건하지만, 3D GS 는 explicit primitive 를 사용하기 때문에 motion blur, rolling shutter 등 image quality 에 극도로 민감하다.
Left: GT, Right: trained 3D GS on motion blurred scene,
source: Deblurring 3D GS -
물리적인 반사 효과 모델링이 힘들다.
Physically-based Rendering 이 아니기 때문에 조명, 반사 효과 등을 모델링하기 힘들다.
Left: GT, Right: 3D GS, source: 3D GS-DR
1), 2) 등에 대해서는 RadSplat 에서 Zip-NeRF 로 Radiance Fields 를 먼저 학습한 후, NeRF scene 에서 perfect & calibrated pinhole image 를 rendering 하여 3D GS 의 training data 로 사용하면서 우회한 바 있다.
하지만 이 학습 방법은 2-stage 기 때문에 효율적이지 못하며, 근본적으로 rasterization 이기 때문에 갖는 3) 은 여전히 challenge 로 남아있다.
2. Background
2.1. Parameterization
Primitive kernel 은 original 3D GS 와 같이 3D 공간에서 covariance matrix 를 통해 정의된다.
Kernel 정의가 같기에 다른 계산들도 3D GS 와 유사하지만, Spherical Harmonics to RGB 계산에 사용되는 direction 에 대해 짚고 넘어갈 차이점이 있다.
3D GS 에서는 camera position $o$, Gaussian means $\mu$ 를 입력으로 받아 direction 을 만들어 이를 SH2RGB 에 이용한다.
즉 실제 pixel 에 투영되는 각도와는 약간 다른 값을 사용하는 것인데, ray direction 을 사용하지 않은 이유는 tile-wise 로 rasterization 을 진행할 때 color 값 등을 미리 저장해두고 사용하기 때문이다. (cf. 3D GS rasterization 분석글)
// in preprocessCUDA
glm::vec3 result = computeColorFromSH(idx, D, M, (glm::vec3*)orig_points, *cam_pos, shs, clamped);
rgb[idx * C + 0] = result.x;
rgb[idx * C + 1] = result.y;
rgb[idx * C + 2] = result.z;- 이렇게 미리 계산해둔 rgb 를 Render kernel 에 입력으로 넣어 pre-computed color 를 사용한다.
이 방법을 사용하면 rendering 속도는 극대화되지만, 3D GS 의 약점 중 하나인 illumination effect modeling 에 더 약점을 보이는 설계가 된다. 3D GRT 에서는 이를 방지하기 위해 SH2RGB 에서 ray direction 을 사용한다고 한다.
2.2. Hardware-Accelerated Ray Tracing
NVIDIA 계열 GPU 는 ray tracing 을 위한 RT cores 가 따로 설계되어 있어, ray 와 particle 의 intersection 은 RT core 가 담당하고, shading 에 해당하는 더 계산량이 높은 작업은 SMs 에게 할당하는 식으로 최적화 되어 있다.
이렇게 설계된 기존 Ray Tracer 들을 사용할 수도 있지만, 이는 주로 opaque particle 을 렌더링하는데 초점이 맞추어 설계되어 있다. 즉, ray traversal 과정에서 예상되는 hit count 가 낮으며, SMs RT 코어 간의 상호 작용이 최소화된다.
하지만 3D Gaussian 의 경우 semitransparent 하기 때문에 이러한 Ray Tracer 가 효율적이지 않고, 따라서 3D Gaussian 을 위한 적절한 Ray Tracing 알고리즘을 설계해야한다.
3. 3D Gaussian Ray Tracing

3D Gaussian 을 위한 Ray Tracer 설계를 위해 다음 두가지의 핵심 요소가 필요하다.
- Hit traversal 가속화를 위해 BVH 를 사용하는데, BVH 를 위한 proxy primitive 를 3D Gaussian 에 알맞게 정의할 것
- 3D Gaussian Ray Tracing 의 rendering algorithm (cast ray & gather information) 을 알맞게 정의할 것. 즉 어떻게 효율적으로 ray 를 samplng 하고 gaussian responce 를 계산할 것인지 결정해야한다.
각 요소에 유의하며 3D GRT 설계를 따라가보자.
3.1. Bounding Primitives
간략하게 BVH (Bounding Volume Hierarchy) 부터 짚고 넘어가자.
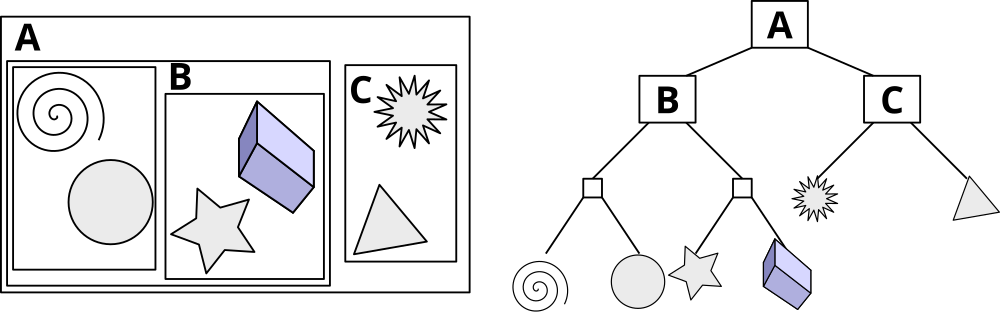
BVH 란, 공간을 분할하여 hierarchy 로 나타낸 tree structure 이다. Parants node 는 더 큰 bounding volumes 으로 leefs 를 완전히 감싸는 형태로 이루어져있으며, 이를 통해 효율적으로 공간을 분할 탐색할 수 있게 된다.
즉 BVH 의 목적은 3D Gaussian 을 적절하게 감싸는 proxy primitive 를 정의하고, 이 proxy geometry 로 BVH 를 구성하여 어떠한 3D Gaussian 들을 ray traversal 과정에서 탐색할 것인지를 결정하는 것이다.
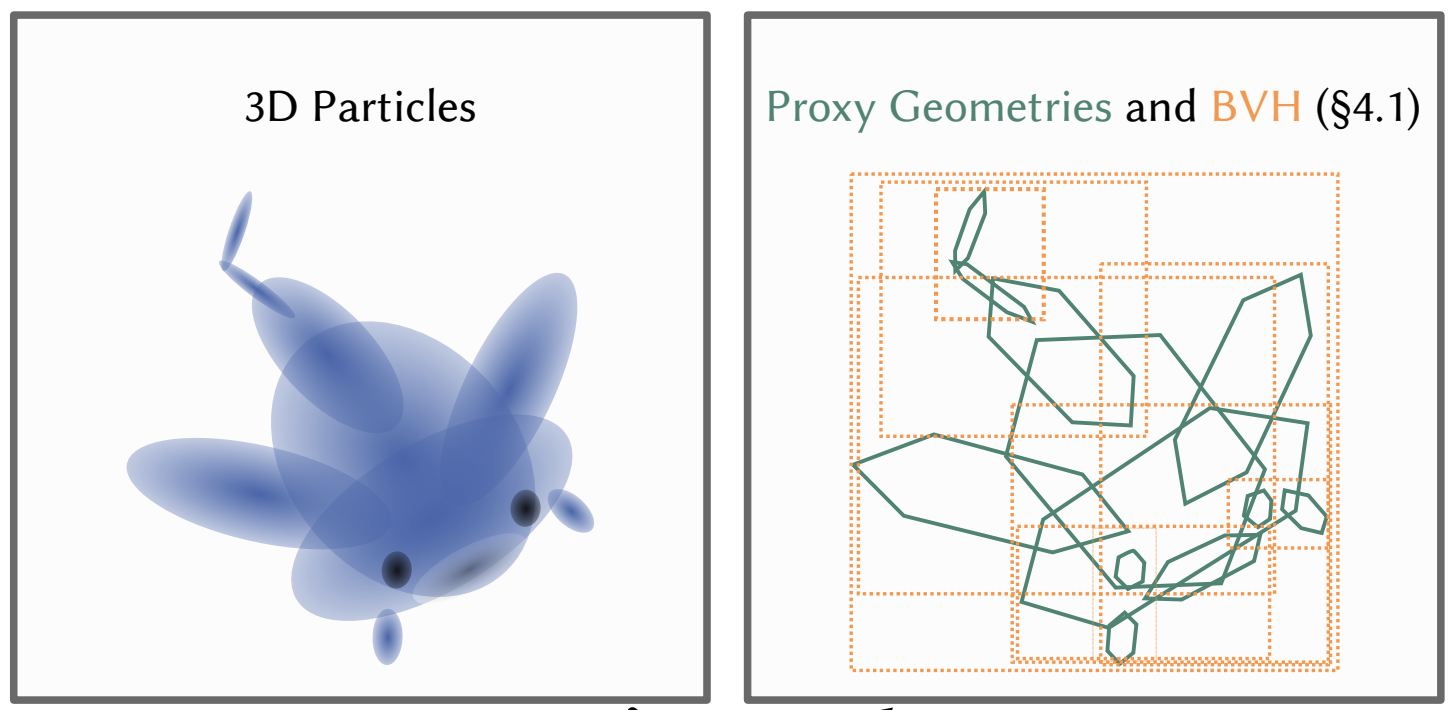
저자에 의하면, NVIDIA OptiX 에서는 미리 정의된 3가지 타입 1) triangle, 2) sphere and 3) AABBs 은 모두 3D Gaussian 에 적절하지 않다고 한다. 3) 의 AABB 를 이용하는 경우를 생각해보면, 계산은 간단하지만 false positive proxy hit 이 많아지기 때문에 trade-off 가 있다 (see Fig. 4).
Stretched Polyhedron Proxy
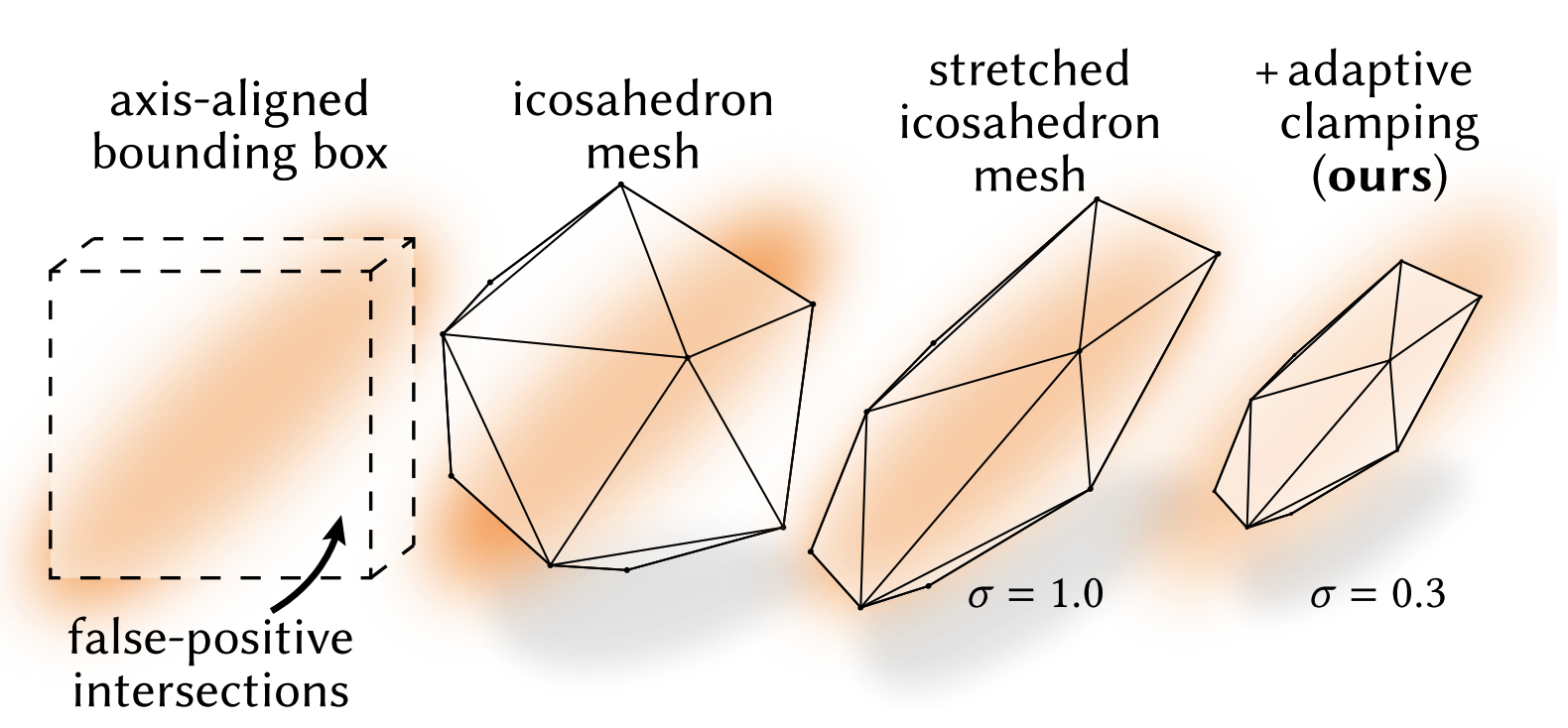
저자들은 실험을 통해 Icosahedron (정이십면체) 를 사용하는 것이 가장 적절했다고 한다.
- Icosahedron 은 triangular face 로 이루어져 있기 때문에 ray-face intersection 을 계산하는 것이 hardware optimized 되어 있다.
- 3D Gaussian 에 대해 false positive, false negative 가 너무 많지 않게 감쌀 수 있는 적절한 모양이다.
Unit sphere 를 내접하는 icosahedron 에 대하여, 3D Gaussian 에 대한 minimum responce alpha (0.01 로 설정) 값을 통해 각 vertex 를 다음과 같이 transform 하여 proxy geometry 를 계산한다.
$$ v \leftarrow v \sqrt{2 \log (\sigma / \alpha_{\min})} \ {\rm SR^T} + \mu $$
논문에 공식만 턱 나와 있어서 당황스러울 수 있는데, 차근차근 분석해보자.
Stretching
먼저 ${SR^{\rm T}}$ 과 $\mu$ 은 3D Gaussian 이 정의된 local coordinate 로의 transform 이다. 즉 init Icosahedron 을 3D Gaussian 에 맞게 이동하고, 적절히 늘리고 회전하는 작업이다.
Adaptive Clamping
scaling 공식을 살펴보면, scale 이 변하지 않을 때가 다음과 같음을 알 수 있다.
$$ \sigma / \alpha_{\min} = \exp(0.5) \ \rightarrow \sigma \cdot \exp (- 1/2) = \alpha_{\min} $$오른쪽 항이 익숙하지 않은가? GS 의 response 형태와 닮아 있다.
$$ f_i(p) = \sigma_i \cdot \exp \left( - \frac{1}{2} (\mu_i -p)^{\rm T} \Sigma_i^{-1} (\mu_i - p ) \right ) $$즉 scale 이 1로 유지되는 기점은 3D Gaussian 의 local coordinate 에서 std 가 1만큼 떨어져 있는 곳의 responce 가 minimum responce 값보다 작은지 큰지를 결정하는 지점이 된다.
0.01 에 대한 당위성이 없다고 생각할 수도 있는데, confidence 99% 정도에 해당하는 std 값 2.6을 통해 gaussian pdf 를 계산해보면 대략 0.01 이란 값이 나온다. 비슷하게 3D GS 에서는 culling 을 위한 radius 계산에 3xstd 값을 이용한다.
$$ \exp\left(-\frac{1}{2}(2.6)^2 \right) \cdot \frac{1}{\sqrt{2 \pi}} \approx 0.01 $$
Adaptive Clamping 는 opacity 까지 scaling 에 함께 활용하기 때문에, 거의 투명하지만 크기는 큰 particle 에 대해서는 실제 proxy primitive 가 작게 설정되는 등의 이점이 존재한다.
3.2. Ray Tracing Renderer
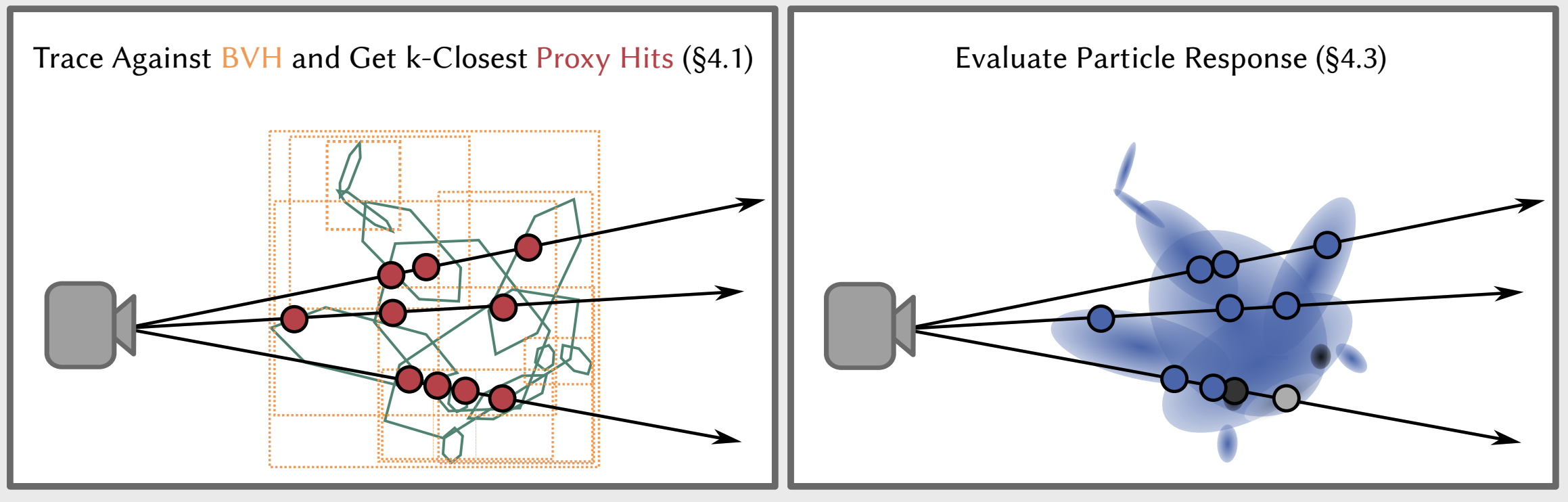
미분 가능하고 효율적인 렌더링을 위해 3D GRT 는 sorted $k$-buffer 를 통해 순차적으로 rendering 을 진행한다.
- BVH 를 이용해 next $k$ closest particle 을 추적하고 (이때는 hit response 를 측정하지 않는다)
- 각 chunk 내에서 실제 hit response 를 iterative 하게 측정한다
- 이때, ray 내의 모든 proxy hit particle 을 검사하거나
- 일정 threshold 에 도달하면 rendering 을 종료한다.
다음 그림은 $k=3$ 일 때 3D GRT 의 ray tracing 과정을 도식화한 것이다.
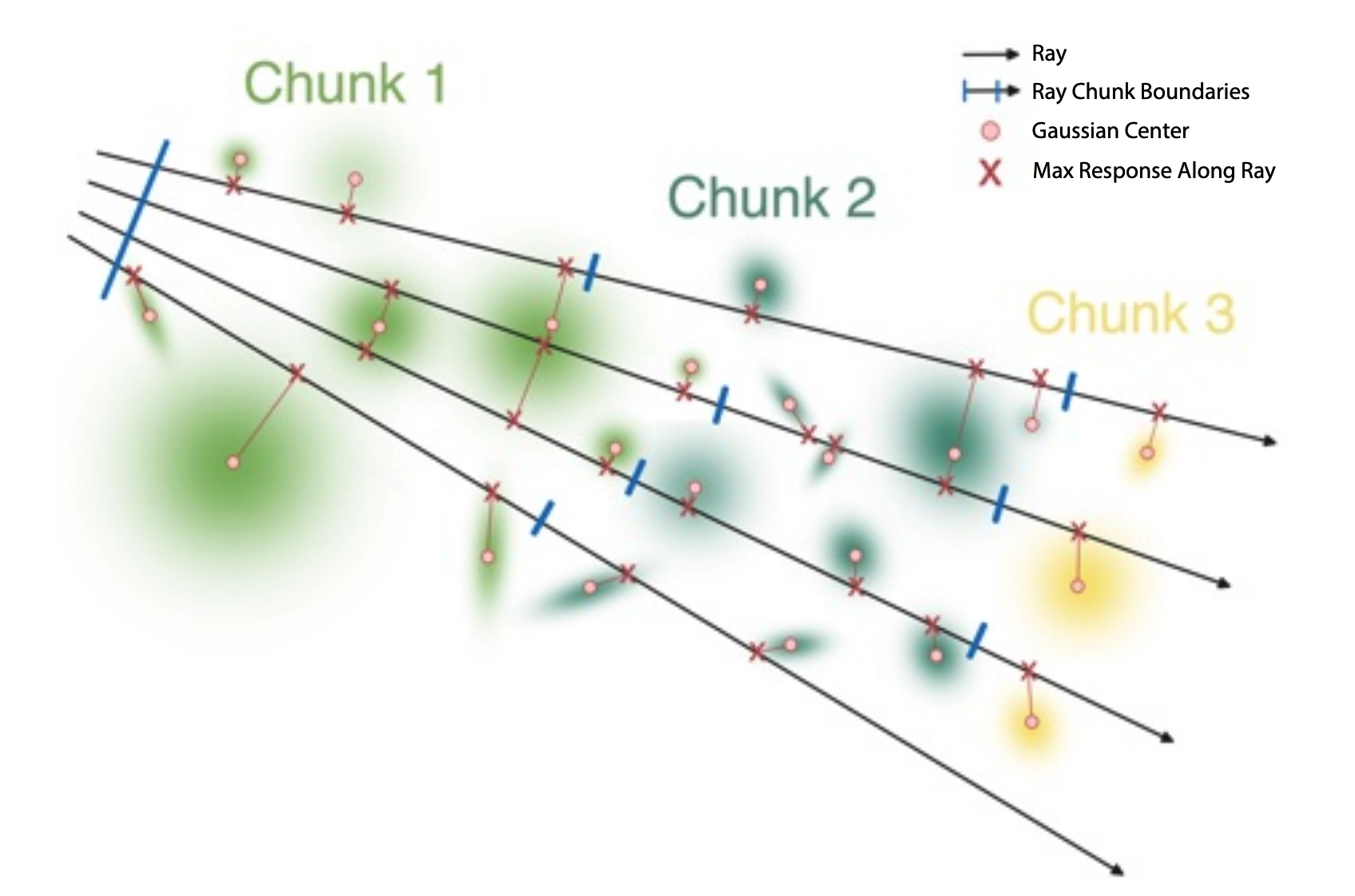
3.3. Ray-Gaussian Intersection
우리는 이제 어떻게 각 particle 의 contribution 을 계산할 것인가를 결정해야 한다. 3D GRT 에서는 이를 입자가 최대 response 가지는 analytic solution 을 제시하여 해결한다.
where $ \mathbf{o}_g = {\rm S^{-1}R^T}(\mathbf{o} - \mu), d_g = {\rm S^{-1}R^T} \mathbf{d}$.
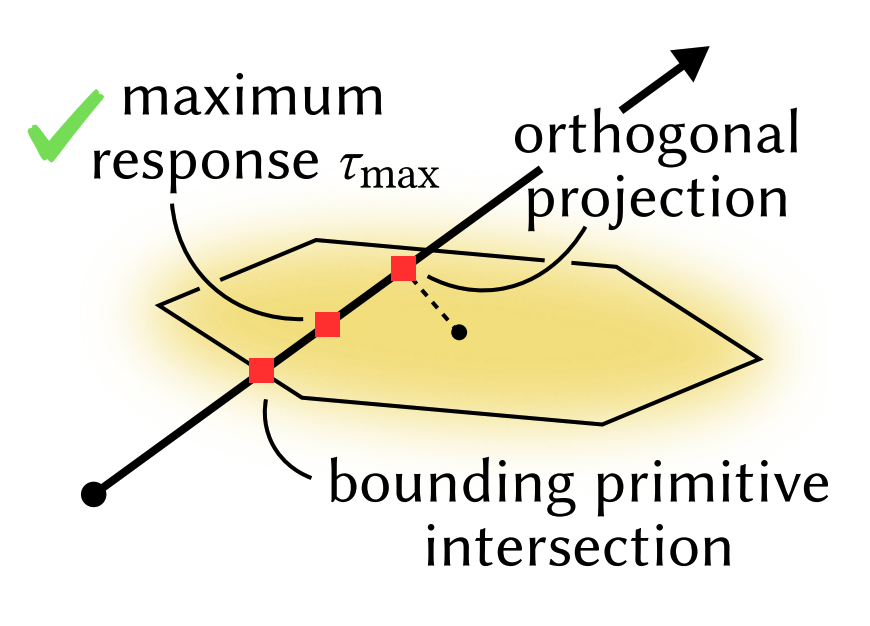
이 또한 당황하지 말고 차근차근 해석해보자.
$\mathbf{o}_g$ 와 $\mathbf{d}_g$ 의 정의를 살펴보면 proxy primitive 정의와 마찬가지로 3D Gaussian 의 local coordinate 로의 transform 된 origin, direction (non-unit vector) 임을 알 수 있다.
즉 우리는 3D Gaussian density 를 다음과 같은 1D Gaussian density 로 쓸 수 있는데,
$e^{-x}$ 는 decreasing function 이므로 inner quadratic term $\mathbf{x}_g^{\rm T} \mathbf{x}_g$ 값이 최소일 때 gaussian density 값이 최대임을 알 수 있다.
즉, 어떤 gaussian 에 대한 maximum density 를 찾는 문제는 다음과 같은 최적화 문제로 볼 수 있으며,
이는 $t$ 에 대한 convex function 이기 때문에 derivative 가 0인 극소점에서 minimum 을 구할 수 있다.
따라서, 논문에 제시된 다음의 공식이 유도된다.
직관적으로 생각해도 자명한데, $\mathbf{o}_g, \ \mathbf{d}_g$ 가 3D Gaussian 이 정의하는 elliptical space 로 transform 되어 있으므로, ray direction 이 3D Gaussian origin 과 align 되어 있을 수록, 거리가 가까울 수록 높은 reponce 를 보이게 된다.
Ray tracing 은 proxy hit 순서로 진행되기 때문에 실제로 ray 에 대한 particle 들의 maximum responce 의 순서와는 약간 다를 수 있지만, 이 approximation 이 성능 저하를 초래하지 않았다고 한다.
4. Experiments
4.1. Quantitative Results
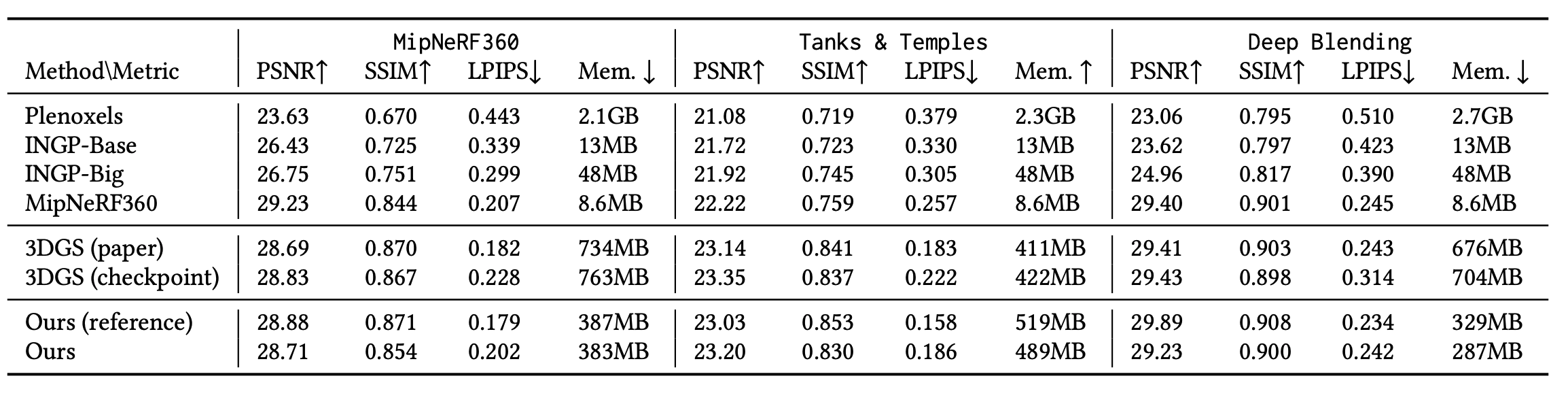
정량적, 정성적 평가 모두 훌륭하게 제시되어 있다. (역시 갓비디아…)
3D GS 와 NVS quantitative results 는 거의 차이나지 않으며, fps 는 조금 느리지만 여전히 real-time 을 달성한다.
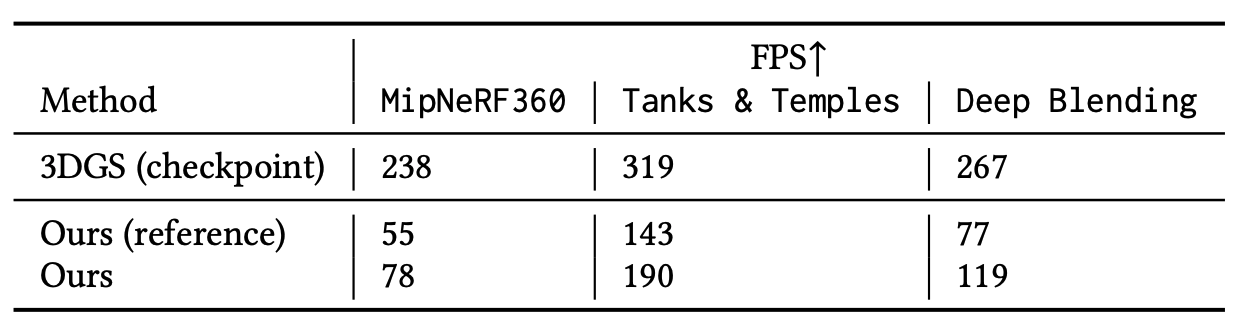
Ablation Study
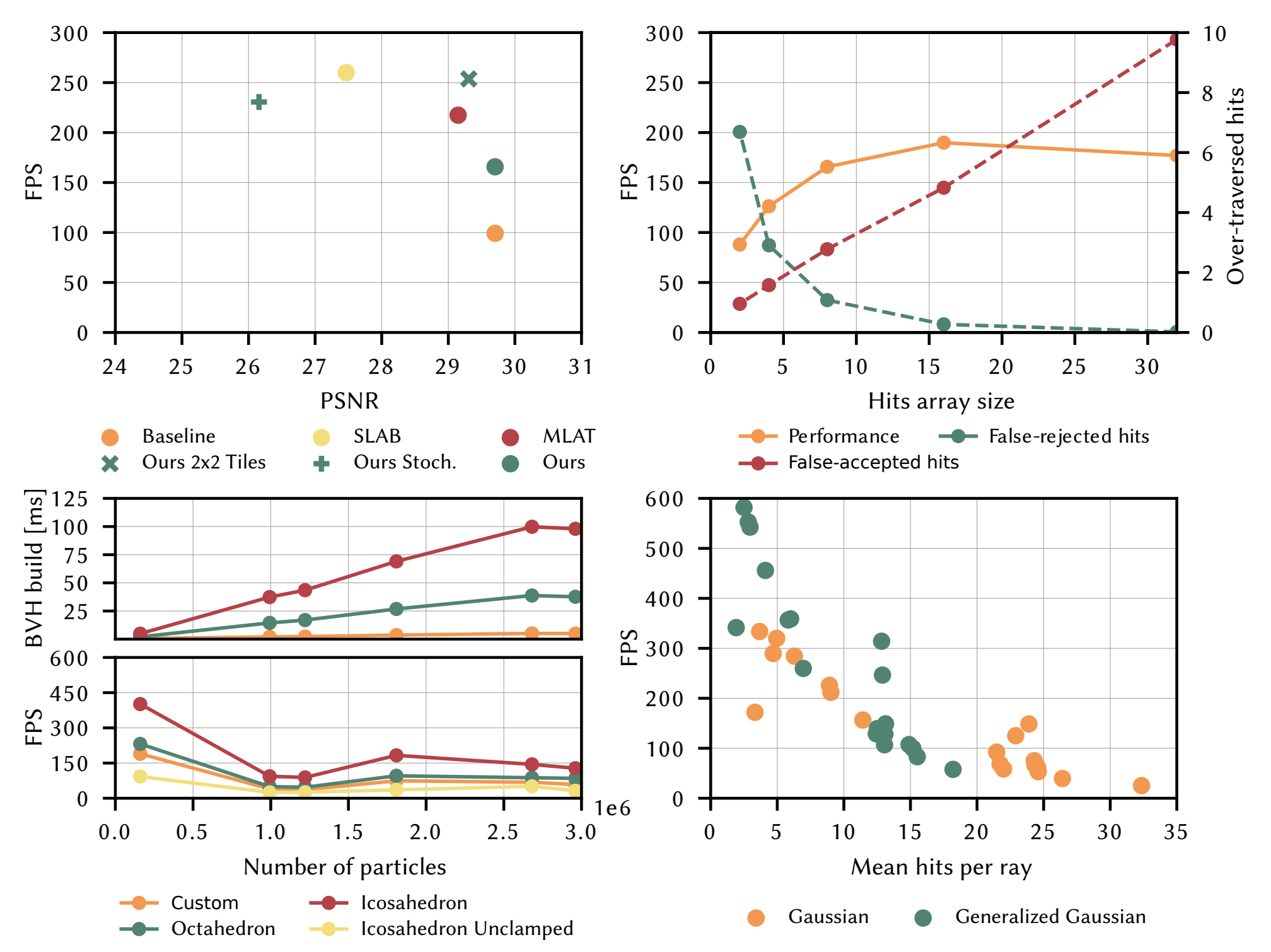
Ablation study 로는 제안한 Next $k$-closest Ray Tracer 와 SLAB, MLAT 등 기존 ray tracer 들과의 비교 (Fig. 8 top left), $k$-buffer proxy mesh design 에 대한 당위성이나 $k$ buffer 에서 적절한 $k$ 값을 설정하는 등의 실험이 보고되어있다.
Particle Kernel Design
설계된 Ray Tracer 에 대해 particle kernel 이 꼭 3D Gaussian 일 필요는 없으므로, 저자들은 다음 네 개의 kernel design 에 대한 실험도 진행하였다.
-
3D Gaussian
$$ \hat{p}(x) = \sigma e^{ -(x-\mu)^{\rm T} \Sigma^{-1} (x-\mu) } $$
-
Generalized Gaussian: generalized of degree $n$
$$ \hat{p}_n(x) = \sigma e^{- \left((x-\mu)^{\rm T} \Sigma^{-1} (x-\mu)\right)^n } $$
-
2D Gaussian: Gaussian Surfels, suggested in 2D Gaussian Splatting (cf. my previous review )
-
Cosine wave modulation: aims to model a particle with spatially varying radiance
$$ \hat{p}_c(x) = \hat{p}(x) \left ( 0.5 + 0.5 \cos (\psi {\rm R^T S^{-1}} (x-\mu)) \right ) $$
정량 평가는 Fig. 10 에서 볼 수 있는데,
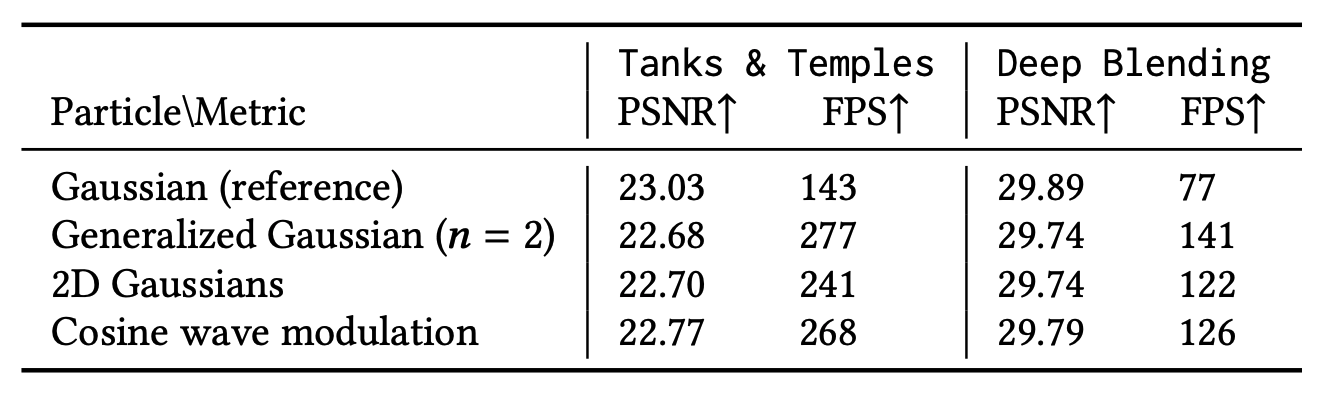
각 kernel 별로 reconstruction 성능은 비슷하나, Generalized Gaussian (GG) 를 사용할 때 fps 가 3D Gaussian 에 비해 2배 가까이 올라간다. 이는 GG 의 kernel design 에서 $e^{-x}$ inner quadratic 을 degree $n$ 으로 제곱하기 때문에 density 가 mean 부근으로 몰려서 opaque particle 에 가깝게 modeling 되기 때문이다.
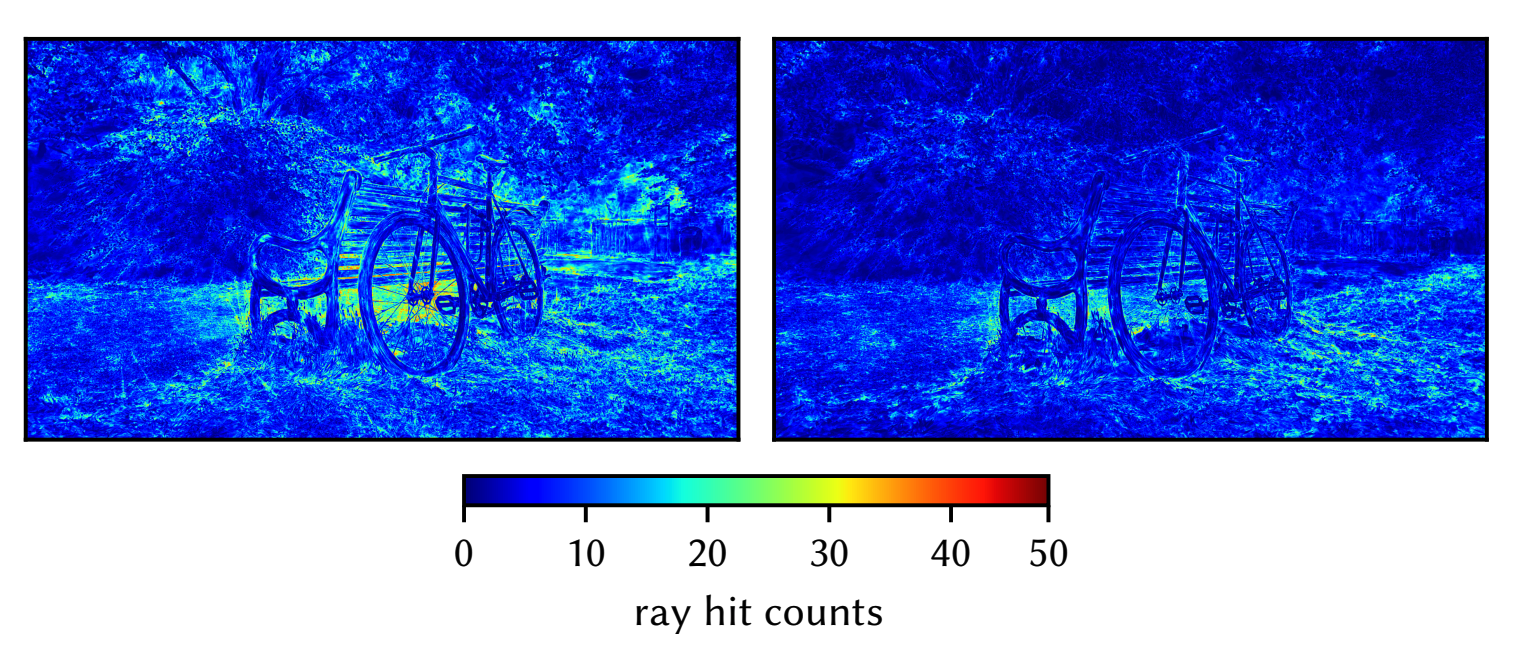
따라서 ray-particle hit 자체가 줄어들 것을 예상할 수 있으며, 이는 실제 저자들이 제공하는 ray-hit visualization 에서도 볼 수 있다.
4.2. Qualitative Results
Qualitative Results 에서는 앞서 지적한 rasterization 의 한계점을 타파한 모습들을 보여준다. 다양한 camera model 에 대한 rendering 및 light effect 를 모델링하는 모습을 통해 3D GRT 가 효과적으로 구현되었음을 입증한다.


5. Conclusion
역시 갓비디아… 역작 논문인 것 같다.
Rasterization 으로 인한 한계는 3D GS 의 단점으로 지속적으로 제기되는 중이고, camera modeling 에 대한 문제나 illumination modeling 등은 각기 다른 하위 주제로써 활발히 후속 연구들이 제시되고 있다.
- 3D Gaussian Splatting with Deferred Reflection
- On the Error Analysis of 3D Gaussian Splatting and an Optimal Projection Strategy
그런데 rasterization 을 사용하는 것에 제한되어 이를 해결하는 대신 ray tracing 을 어떻게 3D Gaussian 에 효율적으로 구현할 수 있을지 치열하게 연구하고 실험한 흔적이 엿보이는 훌륭한 논문이었다.
물론 논문에 언급된 바와 같이 최대한 효율적인 설계를 지향했음에도 rasterization 보다는 느린 속도를 보여준다. 하지만 게임 회사에 재직하면서 neural rendering 관련 연구를 진행하면서 느낀 점인데, 단순히 빠른 속도와 좋은 real world reconstruction 만을 보여주는 3D GS 자체는 사용처가 극히 떨어진다.
따라서 neural rendering 기술을 game/graphics 엔진에서 활용하기에는 확장성이 높은 ray tracing 기반 접근법이 더 효용가치가 높을 것 같다.
You may also like,
- A Comprehensive Analysis of Gaussian Splatting Rasterization
- Under the 3D: Geometrically Accurate 2D Gaussian Splatting