Introduction

3D Gaussian Splatting 의 최대 장점은 그 무엇보다도 100fps 이상의 렌더링 '속도' 이다. 그 어떤 NeRF-based method 보다도 빠른 이 속도는 잘 설계된 tile-based rasterization 덕분인데, 오늘은 이 rasterization 관점에서 3D Gaussin Splatting 을 (최대한) 완벽하게 이해해보는 시간을 갖도록 해보자.
1. 3D Gaussian as Primitive Kernel
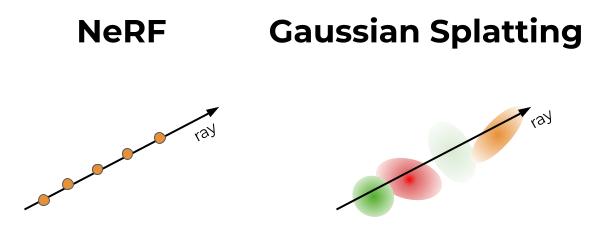
3D Gaussian Splatting 의 기본 idea 는, implicit 한 NeRF 와 다르게 explicit 하고 학습 가능한 primitives 로 scene 을 표현하자는 것이다. (explicit 한 표현으로 갖는 여러가지 장점이 있는데, 이는 저번 2D GS review 에서 언급한 바 있으니 궁금하다면 링크를 참조하기 바란다.)
저자들은 이러한 primitive (particle) 에 대한 kernel 을 다음과 같은 3D Gaussian function 으로 정의하였다.
이 kernel design 에 대해서 꼭 3D Gaussian 이어야 했나? 라는 의문이 들 수 있는데, 논문에 언급된 몇 가지 도입 이유가 있다.
- 학습을 위해 differentiable 할 것
- 빠른 alpha blending 을 위해서 2D 로의 projection 이 쉽고 잘 정의되어 있을 것
해당 기준 정도만 만족하면 어떤 kernel design 을 사용해도 무방할 것 같고, 실제로 최근 3D Gaussian Ray Tracing 에서 여러가지 kernel 로 실험해봤는데, 성능에 큰 차이 없었다고 한다.
Covariance Matrix 는 positive definite 일 때만 물리적인 의미를 가지므로, 저자들은 학습의 용이성을 위해 covariance matrix 를 다음과 같은 형태로 구성할 것을 제안한다.
여기서 $R$, $S$ 는 각각 ${3 \times 3}$ rotation, scale matrix 이다.
이 covariance matrix 를 다음과 같이 약간 바꿔서 쓸 수 있는데, covariance matrix 의 형태가 3D ellipsoid (anistropic) matrix 와 같은 것을 알 수 있다. 즉 3D GS 는 3D 상의 불투명한 (Gaussian Distribution 으로 density 가 정의되는) 타원체를 primitive kernel 로 사용한 것이다.
Tip. Quadratic form $A^{-1}MA$ 을 다룰 때는, $M$ transformation in $A$ coordinate system 이라고 해석하면 좋을 때가 많다. 이는 eigendecomposition 을 해석할 때도 마찬가지인데, 선형변환에도 방향이 보존되는 axis (eigenvectors) 로 이루어진 coordinate system 에서, 각 axis 가 어느 정도의 가중치를 가지고 있는지 (eigenvalues) 분석하는 것이 eigendecomposition 이다. 이렇게 생각하면 PCA 가 왜 eigendecomposition 과 연관있는지 자명하다.
다시 말해, 정의된 Covariance matrix 는
-
ellipsoid 의 각 principal axis 가 basis 인 coordinate system 에서의 intensity matrix (squared scale) 를
-
world coordinate system 으로의 표현 방법
이라고도 해석할 수 있다.
// compute 3D covariance matrix
glm::mat3 S = glm::mat3(1.0f);
S[0][0] = mod * scale.x;
S[1][1] = mod * scale.y;
S[2][2] = mod * scale.z;
glm::mat3 R = glm::mat3(
1.f - 2.f * (y * y + z * z), 2.f * (x * y - r * z), 2.f * (x * z + r * y),
2.f * (x * y + r * z), 1.f - 2.f * (x * x + z * z), 2.f * (y * z - r * x),
2.f * (x * z - r * y), 2.f * (y * z + r * x), 1.f - 2.f * (x * x + y * y)
);
glm::mat3 M = S * R;
glm::mat3 Sigma = glm::transpose(M) * M;
cov3D[0] = Sigma[0][0];
cov3D[1] = Sigma[0][1];
cov3D[2] = Sigma[0][2];
cov3D[3] = Sigma[1][1];
cov3D[4] = Sigma[1][2];
cov3D[5] = Sigma[2][2];
여기서,
- $S$: 3x3 diagonal matrix,
- $R$: quaternion to rotation matrix 공식을 통해서 계산되었다.
$$ R = \begin{bmatrix} 1 - 2y^2 - 2z^2 & 2xy - 2zw & 2xz + 2yw \\ 2xy + 2zw & 1 - 2x^2 - 2z^2 & 2yz - 2xw \\ 2xz - 2yw & 2yz + 2xw & 1 - 2x^2 - 2y^2 \end{bmatrix} $$
- cov3D: symmetric 이므로, right upper triangle 만 저장해도 된다.
2. Splatting (Projection of Primitives)
2.1. Projection
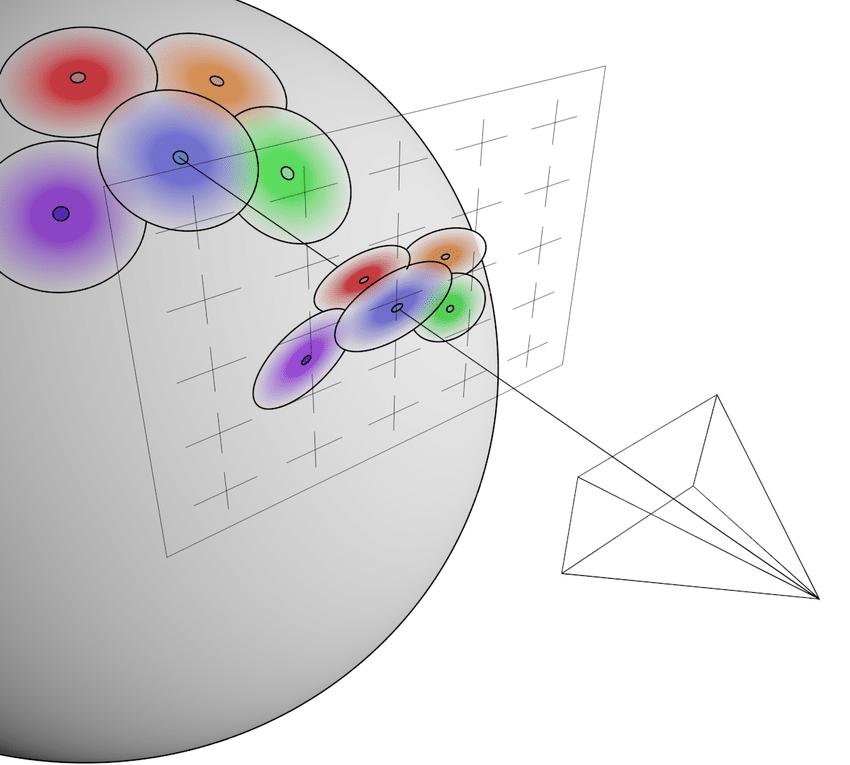
source: Differentiable Surface Splatting for Point-based Geometry Processing
이제 world system 위에 정의된 gaussian 의 covariance matrix 를 image space 에 projection 할 방법이 필요한데, 저자들은 EWA Splatting 에서 제안된, 다음과 같은 방법으로 이를 해결한다.
이 식의 의미를 조금 더 자세히 분석해보도록 하자.
-
이 변환에도 quadratic form 에 대해 같은 해석이 가능하다. 즉, world coordinate system → camera space → ray space 에서의 covariance matrix 를 의미한다.
-
여기서 $J$ 는 Jacobian matrix (affine approximation) of the perspective projection, , 다시 말해 camera → ray space transformation ϕ 에 대한 linear approximation 이다.
$$ \phi(x) = \phi(t) + J \cdot (x - t). $$1st order Taylor approximation 이기 때문에, Gaussian 중심에서 멀어질수록 approximation error 가 생길 것임이 자명하다. 최근에는 이러한 perspective error 를 3D GS 의 한계로 제시하고 해결하려는 연구들도 제시되고 있다. (2D Gaussian Splatting / On the error analysis of 3D Gaussian Splatting)
Perspective projection 에 대한 Jacobian $J$ 는 다음과 같이 유도되며,
실제 구현에서는
-
the image space pixel $(u,v)$ in a pinhole camera model,
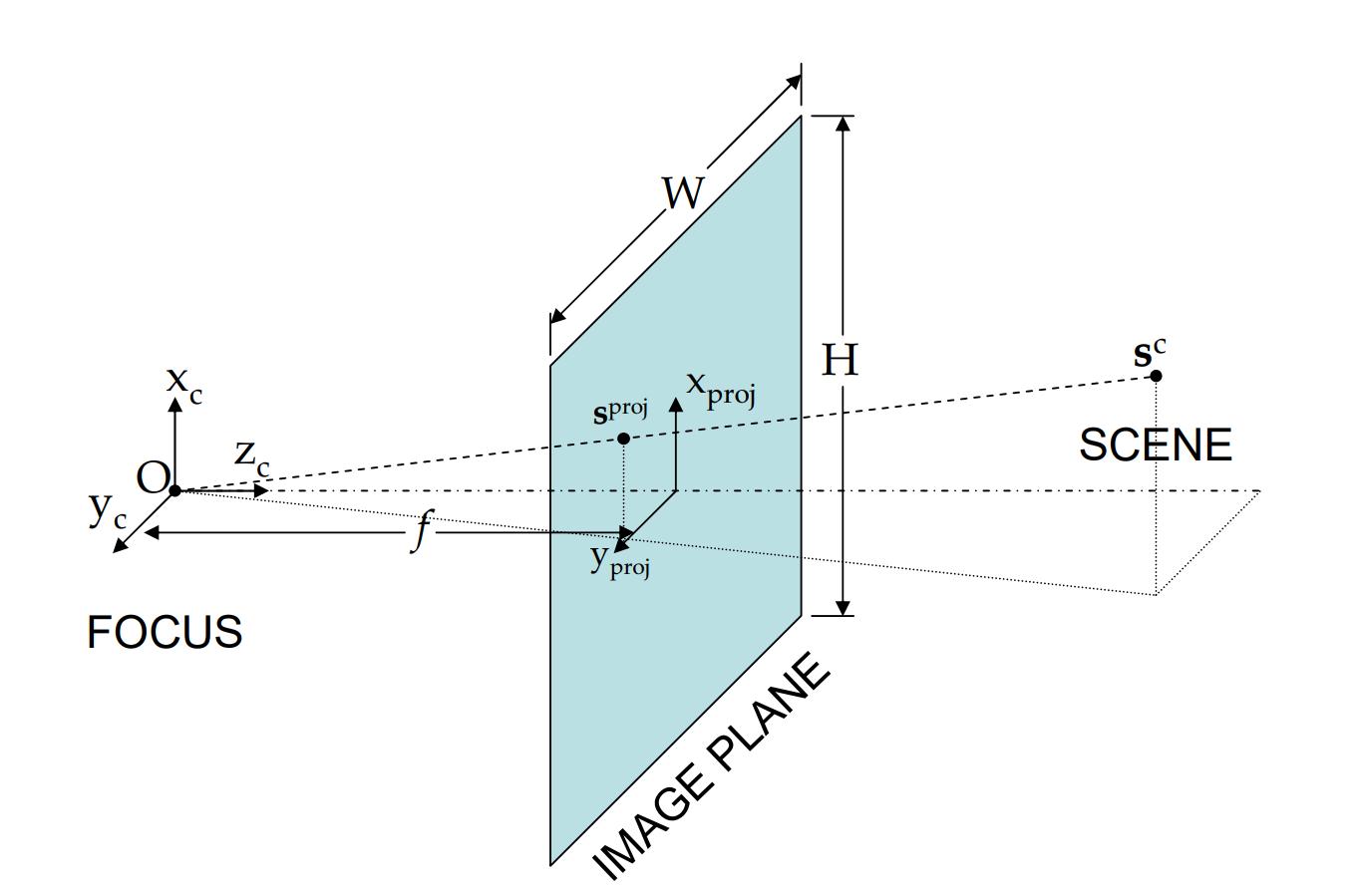
Figure 4. Pinhole camera model, by Fusion of Imaging and Inertial Sensors for Navigation -
image space 에서 필요한 covariance matrix 는 2x2 형태이기 때문에 projection 된 covariance 의 3rd row (z-axis) 는 실제로 사용되지 않으므로
아래의 형태로 구현되어 있다.
// affine approximation of the Jacobian matrix of viewmatrix to rayspace
glm::mat3 J = glm::mat3(
focal_x / t.z, 0.0f, -(focal_x * t.x) / (t.z * t.z),
0.0f, focal_y / t.z, -(focal_y * t.y) / (t.z * t.z),
0, 0, 0);
// W: w2c matrix
glm::mat3 W = glm::mat3(
viewmatrix[0], viewmatrix[4], viewmatrix[8],
viewmatrix[1], viewmatrix[5], viewmatrix[9],
viewmatrix[2], viewmatrix[6], viewmatrix[10]);
glm::mat3 T = W * J;
glm::mat3 Vrk = glm::mat3(
cov3D[0], cov3D[1], cov3D[2],
cov3D[1], cov3D[3], cov3D[4],
cov3D[2], cov3D[4], cov3D[5]);
glm::mat3 cov = glm::transpose(T) * glm::transpose(Vrk) * T;
2.2. Density of the Projected Gaussian
실제 rendering 시에는 Gaussian density 값과 opacity 값을 곱하여 사용하기 때문에, 3D 공간 위의 점 $p$ 에 대해, $i$th Gaussian 의 density $f_i(p)$ 를 다음과 같이 정의할 수 있다.
렌더링 과정에서는 이 density 값에 opacity 를 곱하여 일종의 response 값으로 사용하게 된다.
-
이는 multivariate (3D) normal distribution 에 대한 weighted (by opacity) probability density function 라고도 볼 수 있다.
-
inner exponential 의 값은 Mahalanobis Distance 인데, 3D 상에서 이 값은 scale 을 고려한 ellipsoid 내에서 거리 ( Similarity) 라고 볼 수 있다. 즉, 어떤 3D 상의 point 에서, Gaussian 과 가까울수록, Gaussian 이 opaque 할수록 response 가 커야하는 직관과 정확히 일치한다.
위 density 값을 계산하려면 projection 된 covaraiance 의 inverse matrix 가 필요하다. 코드 상으론 inverse 를 구하는 과정에서 선형대수를 이용한 트릭이 좀 있으니 살펴보도록 하자.
앞서 계산한 2D covariance matrix 를 구하는 함수 끝이 실제로는 다음과 같으며,
// compute cov 2D
cov[0][0] += 0.3f;
cov[1][1] += 0.3f;
return { float(cov[0][0]), float(cov[0][1]), float(cov[1][1]) };
이는 아래 식의 inverse matrix 를 구하는 것과 동일한 것을 알 수 있다 $(A=(RS)^{\rm T})$.
$$ A^{\rm T}A+\lambda \mathbf{I} $$
covariance matrix 가 positive semidefinite 이기 때문에, small $\lambda$ 를 더해주면 다음과 같이 covariance matrix 가 positive definite 이 되므로 inverse matrix 를 구할 때 numerical unstability 가 방지된다.
// compute inverse of the covariance 2D
float det = (cov.x * cov.z - cov.y * cov.y);
if (det == 0.0f)
return;
float det_inv = 1.f / det;
float3 conic = { cov.z * det_inv, -cov.y * det_inv, cov.x * det_inv };
-
2x2 matrix 의 inverse matirx formula 는 다음과 같음을 기억하자
$$ A=\begin{bmatrix} a & b \\ b & c \end{bmatrix}, \quad A^{-1} = \frac{1}{\det(A)} \begin{bmatrix} c & -b \\ -b & a \end{bmatrix} $$ -
또한 cov 의 inverse 를 conic 이라고 명명하고 있는데, 이는 아마 ellipsoid 등이 conic section 으로 정의되기 때문인 것 같다.
마지막으로 각 splats 의 radius 를, 99.7% 이상 cover 가능한
으로 정의해서, 이 값을 Gaussian culling (masking) 하는 용도로 사용한다. (그렇지 않으면 scene 안의 모든 Gaussian 에 query 해야 한다….)
Covariance matrix 로 정의된 3D Gaussian 의 standard deviation 은 eigenvalue 와 같으므로, 다음의 Characteristic equation 을 푸는 것으로 standard deviation 을 구할 수 있다.
이는 $\lambda$ 에 대한 2차 방정식이므로, 너무나 유명한 closed form solution (근의 공식) 이 존재한다 :) 코드에도 근의 공식을 통해 lambda 값을 구하도록 되어있다.
// compute inverse of the covariance 2D
float mid = 0.5f * (cov.x + cov.z);
float lambda1 = mid + sqrt(max(0.1f, mid * mid - det));
float lambda2 = mid - sqrt(max(0.1f, mid * mid - det));
float my_radius = ceil(3.f * sqrt(max(lambda1, lambda2)));
3. Parallel Rasterization
Gaussian kernel 의 정의와, 이 kernel 이 image space 상에 어떻게 projection 되는지 알고 있으므로, 이제 우리는 ray 와 intersect 하는 Gaussian 들에 대해 density 와 opacity 값을 depth order 로만 정렬해서 모으면 3D GS scene 을 2D image 로 그릴 수 있다.
3D Gaussian Splatting 은 이러한 rendering 작업을 효율적으로 하기 위하여 image space (screen) 에 모든 3D Gaussian 을 projection 한 후, 작은 단위의 tile 로 나누어서 각 tile 마다 color / opacity accumulation 을 병렬로 실행하는 tile-based rasterization 을 제시하였다.
논문에 제시된 Rasterization algorithm 을 step-by-step 으로 분석해보도록 하자.
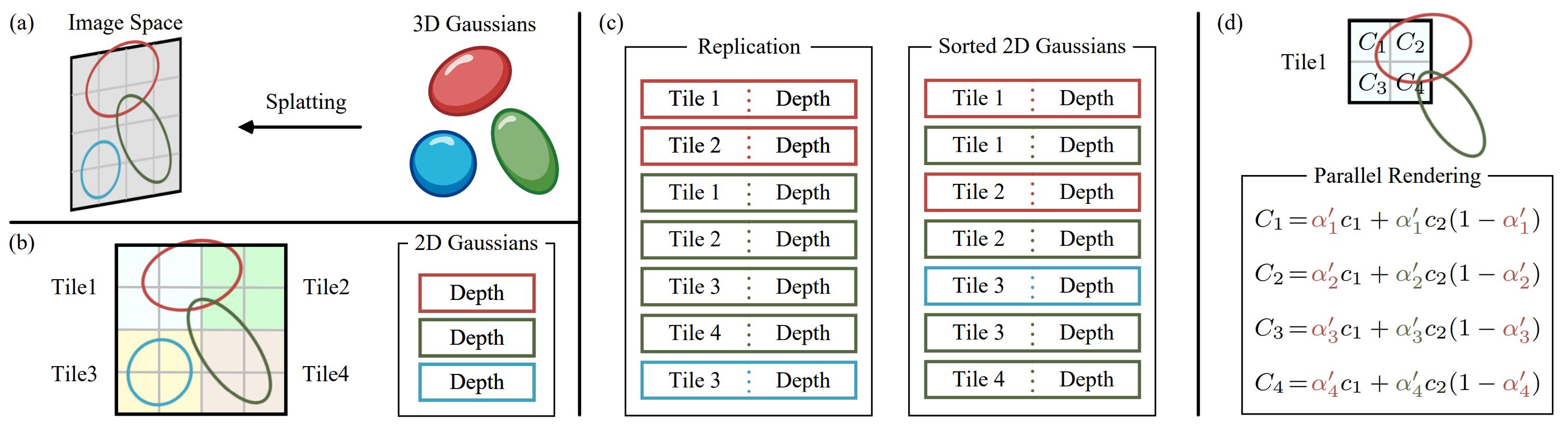
source: A Survey on 3D Gaussian Splatting
-
Screen 을 16x16 크기의 tile 로 나눈다.
이는 CUDA 병렬화 작업을 위해 (전체 tile 개수, 256) 의 grid, thread block 으로 나누어 rasterization 을 진행하기 위함이다. -
Frustum culling 으로 valid gaussian 만 남긴다. (See fig.)
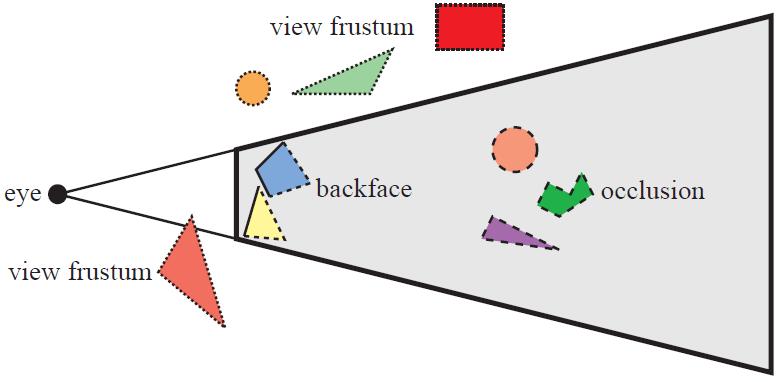
-
Tile 마다 겹치는 Gaussian 은 복제하여 사용한다. (Instantiate)
-
(각 tile 에서) Gaussian 을 depth order 로 정렬한다 (using GPU radix sort)
- Rendering 할 때 사용하는 covariance 가 이미 image space 에 projection 된 상태이므로, depth 로 sort 하지 않으면 순서 없이 이리저리 겹쳐져 있는 모습과 같을 것이다.
- 이 sorting 은 각 thread block 실행 전에 진행되어 tile 단위로는 sort 를 진행하지 않는다. 즉 pre-sort primitives!
-
정렬된 Gaussian 를 통해 각 tile 마다 작업 범위를 설정하고, Tile 마다 one CUDA thread block 을 실행하여 병렬로 rasterize 를 진행한다.
- 각 thread block 은 메모리 병목을 줄이기위해 몇 가지 정보를 shared memory 에 저장해놓는다.
- 정렬된 Gaussian 을 따라서 opacity, color 를 accumulate 하여 최종 color 값을 계산한다.
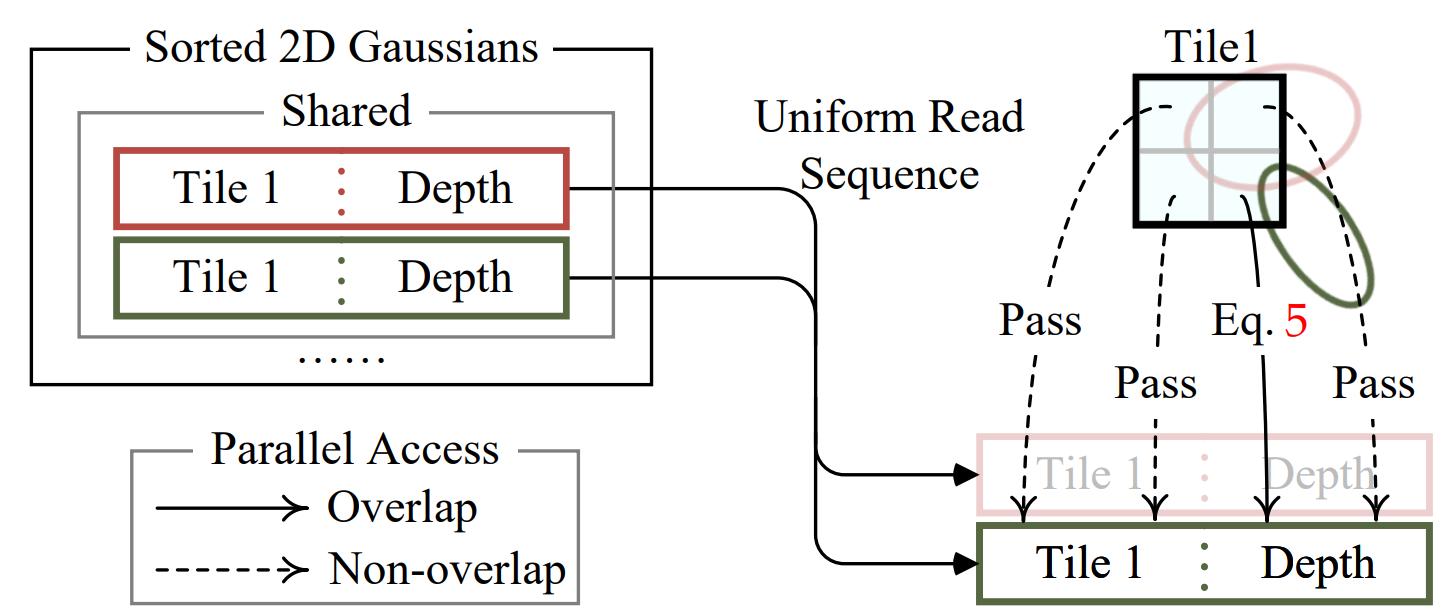
Figure 6. An illustration of the tile based parallel rendering,
source: A Survey on 3D Gaussian Splatting
__shared__ variable 에 실제로 id, opacity, pixel coord 등의 값을 저장해놓고 있도록 구현되어 있다. 즉 Gaussian 의 projected covariance, spherical harmoics color 등은 tile 단위의 계산이 일어나기 전에 이미 계산을 마치고 shared memory 에 저장되어 있다.
// Allocate storage for batches of collectively fetched data.
__shared__ int collected_id[BLOCK_SIZE];
__shared__ float2 collected_xy[BLOCK_SIZE];
__shared__ float4 collected_conic_opacity[BLOCK_SIZE];Also, The color accumulation process, which calculates the final color at pixel $x$ can be mathematically expressed as:
또한 (5) 의 color 계산을 위한 accumulation 과정을 공식으로 써보면 다음과 같은데,
여기서도 NeRF 와의 차이점을 볼 수 있다.
-
Ray 를 따라 point 를 sampling 하여 그 point 의 opacity / color 를 MLP 에 query 해야하는 NeRF 와 달리,
-
3D GS 에서는 이미 tile 에 projection 된 N 개의 splats 를 depth order 로 탐색하면서 opacity / color 를 합한다.
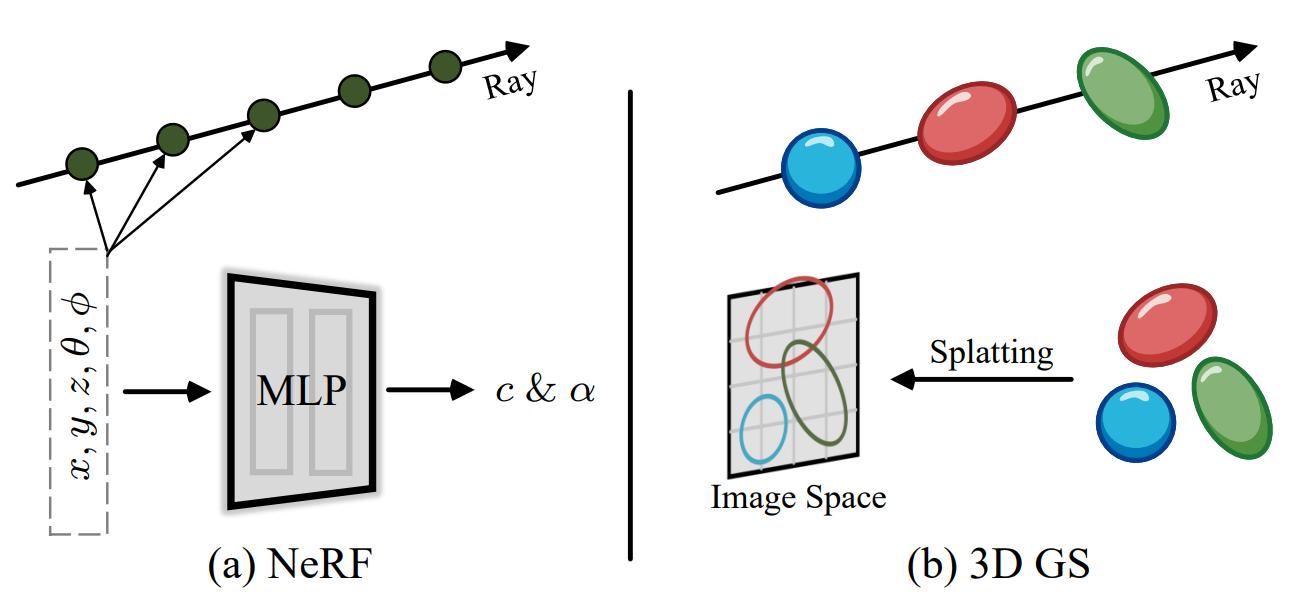
즉 NeRF 에서는 ray 를 sampling 하기 때문에 $r(t)$ 로 sampling 된 각각 다른 point 를 MLP 에 query 하지만, 3D GS 는 모두 똑같은 점 $x$ 를 query 하는 것을 볼 수 있다.
4. Miscellaneous
4.1. Camera Model
현재 구현상으로는 $J$ 가 pinhole camera model 의 perspective projection 으로 구현되었기 때문에 다른 camera model 로 rendering 이 불가능하지만, $J$ matrix 를 알맞은 camera model 에 대해 modeling 하면 원하는 camera model 에 대한 rendering 이 가능하다.
일례로, spherical camera model (e.g., equirectangular) 에 대한 matrix J 를 다음과 같이 modeling 할 수 있는데,
float t_length = sqrtf(t.x * t.x + t.y * t.y + t.z * t.z);
float3 t_unit_focal = {0.0f, 0.0f, t_length};
glm::mat3 J = glm::mat3(
focal_x / t_unit_focal.z, 0.0f, -(focal_x * t_unit_focal.x) / (t_unit_focal.z * t_unit_focal.z),
0.0f, focal_x / t_unit_focal.z, -(focal_x * t_unit_focal.y) / (t_unit_focal.z * t_unit_focal.z),
0, 0, 0);이를 통해 다음의 360 image 를 3D GS 를 통해 training / rendering 이 가능하다.
| 360 Image | Rasterization |
|---|---|
 |
 |
물론 이 경우에는 approximation error 가 perspective projection 보다 훨씬 커지게되어 PNSR 이 pinhole images 를 사용할 때보다 낮아지게 된다. affine projection 을 사용하지 않고 rendering 을 구현하여 camera modeling 하는 방법도 있지만 이는 추후 소개하도록 하겠다.
4.2. Mimic Luma AI
글 Teaser 의 동영상은 NeRFStudio 팀이 창업한 Luma AI 의 rendering 영상인데, 꽤나 팬시해서 따라해보았다. 다음과 같은 과정을 통해 비슷하게 그릴 수 있다.
- Near -> Far plane 으로 black background 에 pointcloud 만 loading 해서 rendering
- Center (training camera 의 mean 으로 잡았음, 직접 설정해도 무방) 으로 부터 radius 를 키우면서 sphere 안의 splats 만 원래대로 rendering
| Scene #1 |  |
|---|---|
| Scene #2 |  |
Closing
알고리즘의 많은 부분을 MLP 에 맡기는 NeRF 의 경우, Linear Algebra 나 Computer Graphics 관점에서 코드가 어떻게 짜여져 있는지 분석하는 것이 쉬운 편인데, 3D Gaussian Splatting 의 경우 explicit 한 primitive 를 다루기 때문에 rasterization module 이 매우 섬세하게 설계되어 있어 수학적, 코드적 관점으로 분석하기 꽤나 난해한 것 같다.
이번 글은 inria group 의 diff-gaussian-rasterizer 의 forward 함수 위주로 분석하였는데, 실제 구현에는 Spherical Harmonics 로부터 RGB color 를 계산, CUDA thread block 할당 및 rasterization 과정에 대한 backward 또한 포함되어 있다. Backward 는 앞서 설명한 forward 계산의 역과정에 가까우며, forward step 에서 front-to-back 으로 탐색하는 것과 반대로 back-to-front 로 탐색하면서 gradient 를 계산한다.
You may also like,
- Don't Rasterize But Ray Trace Gaussian
- Under the 3D: Geometrically Accurate 2D Gaussian Splatting
- A Comprehensive Overview of Gaussian Splatting
- Gaussian Splatting Notes